Предмет: Математика,
автор: motorny0919
Найти общее решение уравнения.
Приложения:
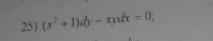
Ответы
Автор ответа:
3
Ответ:
Похожие вопросы
Предмет: Математика,
автор: naxçivanski69
Предмет: Физика,
автор: Ислам333777
Предмет: Русский язык,
автор: Андрей535еноен
Предмет: Физика,
автор: MLGboy47272
Предмет: Математика,
автор: liuda87