Question

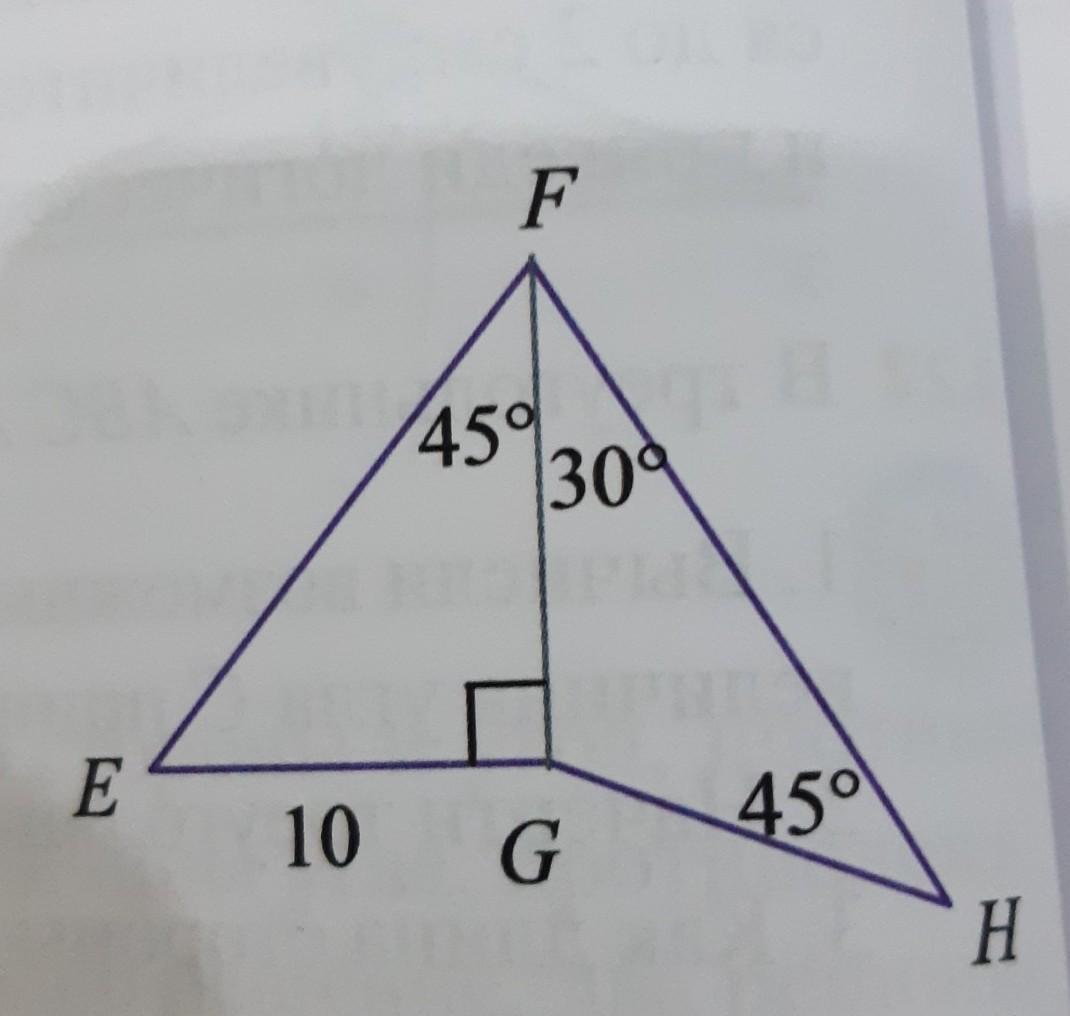
Диагональ FG четырехугольника
EFHG на рисунке 12 перпендикулярна
стороне EG и образует со сторонами
EF и FH углы соответственно рав-
ные 45° и 30°. EG = 10, уголFHG = 45°.
Найди :
1)длину стороны GH.
2)длину стороны FH.
3)Площадь треугольника .​

Answer 1

Ответ:

FH≈14; GH≈7; S=120

Пошаговое объяснение:

∠FEG=180-90-45=45°

∠FEG=∠EFG ⇒ EG=FG

По Теореме синусов $\frac{EG}{sin 45}$=$\frac{EF}{sin 90}$=$\frac{FG}{sin 45}$≈14.142 ⇒ EF≈14

Рассмотрим Δ FGH

∠FGH=180-45-30=105.

По Теореме синусов $\frac{FG}{sin 45}$=$\frac{FH}{sin 105}$=$\frac{GH}{sin 30}$⇒ FH≈14; GH≈7

S ΔEFG= 50, S ΔFGH= 70 ⇒ S EFGH=120