1)Дано: ∠A = ∠B, СО = 4, DO = 6, АО = 5 (рис. 7.54). Найти: а) ОВ, б) АС, BD: в) SAOC, SBOD.
2)В треугольнике АВС АВ = 4 см, ВС = 7 см, АС = 6 см, а в треугольнике MNK МК = 8 см, MN = 12 см, KN = 14 см. Найдите углы треугольника MNK, если ∠A = 80°, ∠B = 60°.
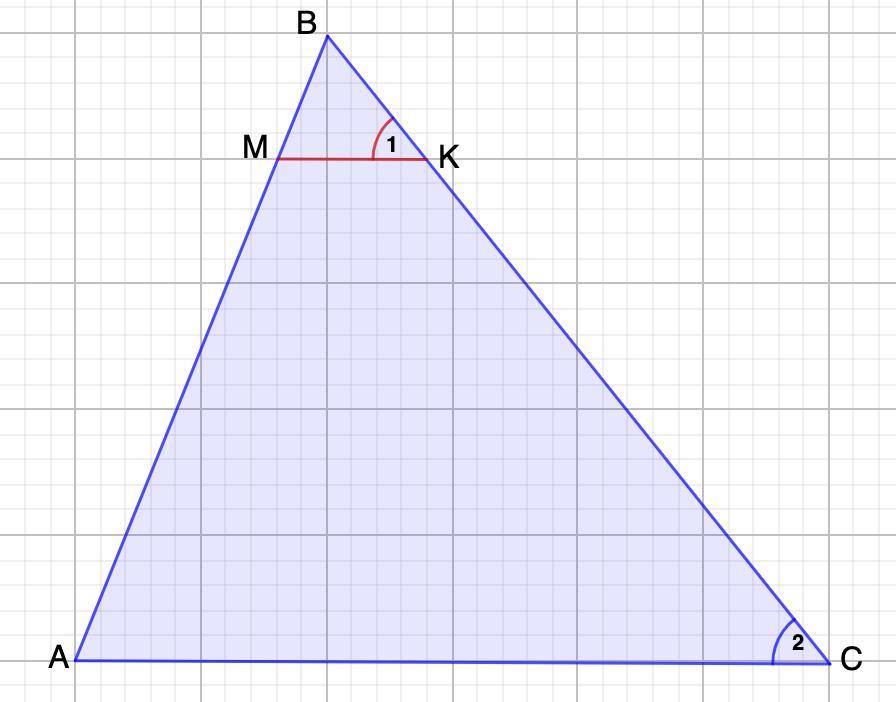
3)Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК||АС, ВМ : AM = 1 : 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см.
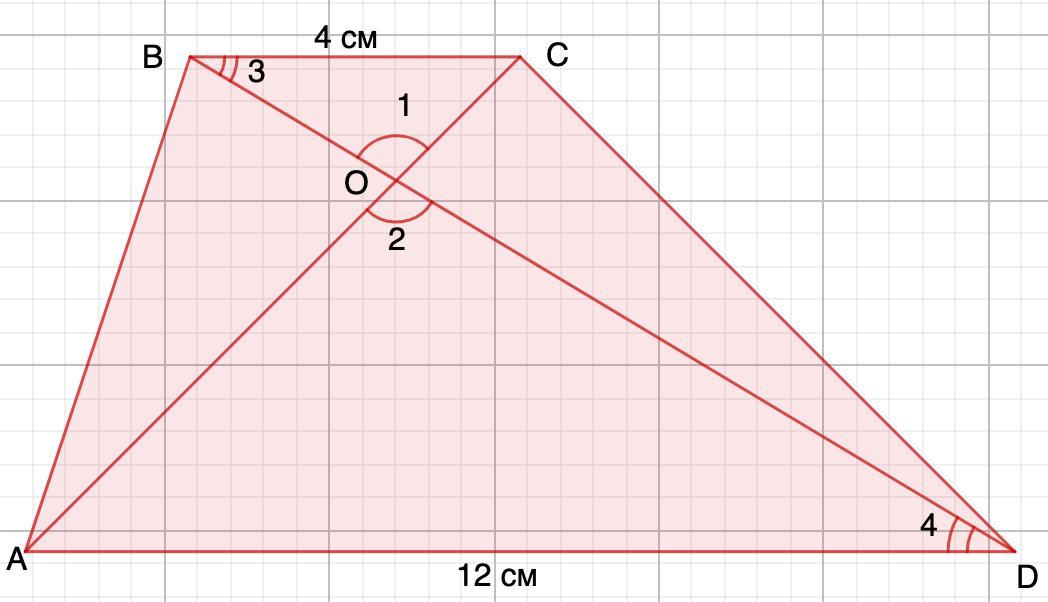
3)В трапеции ABCD (AD и ВС основание) диагонали пересекаются в точке О, AD = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника AOD равна 45 см2.
Ответы
Объяснение:
Уточненное условие.
1) Дано: ∠A=∠B, CO=4, DO=6, AO=5.
Найти: OB,
AC:BD;
Решение:
Рассмотрим ΔАСО и ΔОВD.
∠А=∠В (условие)
∠1=∠2 (вертикальные)
⇒ ΔАСО ~ ΔОВD (по двум углам)
Составим отношения сходственных сторон:
Найдем ОВ:
OB=7,5 (ед)
Коэффициент подобия - отношения сходственных сторон.
⇒ АС:BD=2:3
Площади подобных треугольников относятся как квадрат коэффициента подобия.
⇒
S(ΔAOC):S(ΔBOD)=4:9
2) Дано: ΔАВС и ΔMNK.
AB=4см; ВС=7см; АС=6см;
MK=8см; MN=12см; KN=14см.
∠А=80°; ∠В=60°.
Найти: углы ΔMNK.
Решение:
Рассмотрим ΔАВС и ΔMNK.
⇒ΔАВС ~ ΔMNK (три стороны одного треугольника пропорциональны трем сторонам другого треугольника)
В подобных треугольниках против сходственных сторон лежат равные углы.
В ΔАВС: ∠С=180°-(∠А+∠В)=180°-140°=40°
⇒ в ΔMNK:
∠M=∠A=80°; ∠N=∠C=40°; ∠K=∠B=60°.
3) Дано: ΔАВС.
МК║АС; ВМ:АМ=1:4
Найти:
Решение:
Рассмотрим ΔАВС и ΔМВК.
∠В - общий
∠1=2 (соответственные при МК║АС и секущей ВС)
⇒ ΔАВС ~ ΔМВК (по двум углам)
Пусть ВМ=х, тогда АМ=4х ⇒ АВ=5х.
Найдем коэффициент пропорциональности:
Отношение периметров подобных треугольников равно коэффициенту подобия.
Р(ΔМВК)=5 см
4) Дано: ABCD - трапеция
AD=12 см; ВС=4 см.
Найти:
Решение:
Рассмотрим ΔВОС и ΔAOD.
∠1=∠2 (вертикальные)
∠3=∠4 (накрест лежащие при ВС║АD и секущей ВD.
⇒ ΔВОС ~ ΔAOD (по двум углам)
Найдем коэффициент подобия:
Площади подобных треугольников относятся как квадрат коэффициента подобия. ⇒
S(ΔBOC)=5 см²