Предмет: Геометрия,
автор: oladolisnak0
Висота прямокутного трикутника, проведена до гіпотенузи,
ділить її на відрізки завдовжки 5 см і 20 см. Знайдіть катети
трикутника.
k3nikkov:
а можешь написать на русском?
Ответы
Автор ответа:
6
Ответ:
Катеты треугольника равны см и
см.
Объяснение:
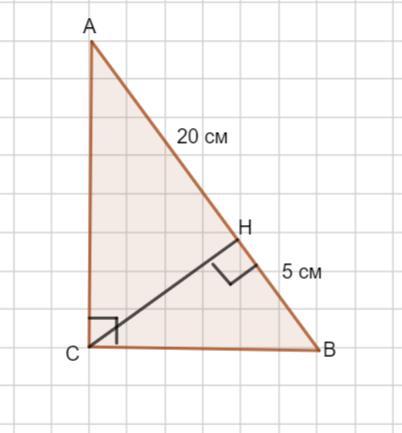
Пусть дан треугольник Δ АВС . В нем проведена высота СН. Точка Н делит гипотенузу на два отрезка, длины которых известны по условию
АН= 20 см, НВ= 5 см.
Тогда гипотенуза АВ= АН+НВ = 20+5= 25 см.
Катет прямоугольного треугольника есть среднее пропорциональное( среднее геометрическое) между гипотенузой и проекцией этого катета на гипотенузу
см
cм.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Ленгит
Предмет: Химия,
автор: menosgrand666
Предмет: Английский язык,
автор: mai8984
Предмет: Математика,
автор: ТСТ1
Предмет: Русский язык,
автор: Мотяндро