Предмет: Алгебра,
автор: aspdkojkasiop
помогите решить пожалуйста
Приложения:
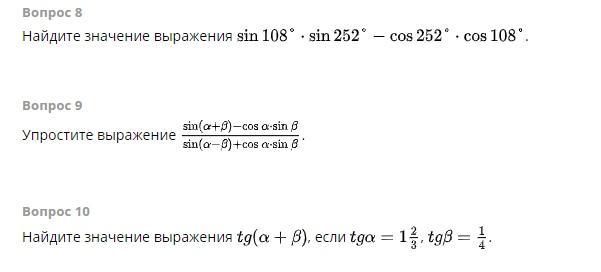
Ответы
Автор ответа:
0
Ответ:
8.
9.
10.
Похожие вопросы
Предмет: Русский язык,
автор: 1olegovna99
Предмет: Литература,
автор: астх
Предмет: Биология,
автор: taki85
Предмет: Литература,
автор: кошарикришарик
Предмет: Қазақ тiлi,
автор: bdanil07