Предмет: Математика,
автор: MaxKing333
Решите плиз⚡ номер тот что обвели
Приложения:
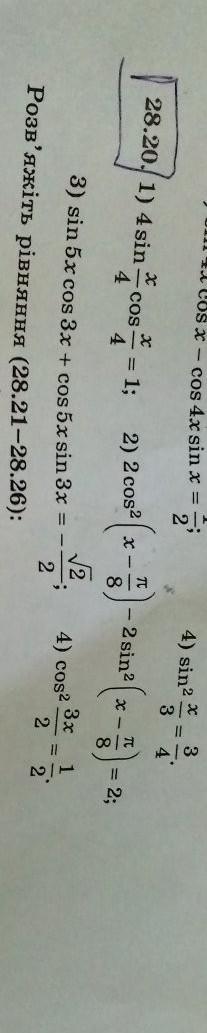
Ответы
Автор ответа:
0
Ответ:
1.
1
2
3
4
n принадлежит Z.
Похожие вопросы
Предмет: Физика,
автор: ромчик13
Предмет: Алгебра,
автор: usmanfatima61
Предмет: Математика,
автор: chernovroal
Предмет: Українська мова,
автор: wast23745
Предмет: История,
автор: Жанетаэ