1. Определить модуль и направление суммарного вектора, используя данные из условия задачи F1=10; F2= 8 и α = 60 градусов
Ответы
Дано:
F1 = 10 H
F2 = 8 H
α = 60°
|R| - ?
Решение:
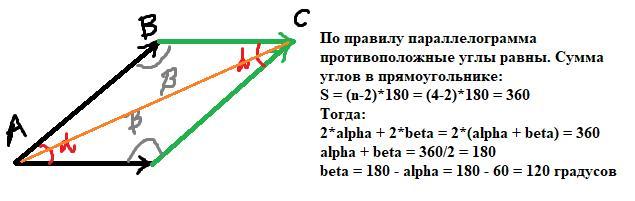
Равнодействующую построим по правилу параллелограмма (смотри рисунок). Равнодействующая - это получившаяся диагональ в параллелограмме. Найдём её, используя теорему косинусов. Диагональ - это основание AC треугольника ABC. Сила F1 - это сторона AB, cила F2 - сторона BC, угол между силами - угол β. Уравнение:
a² = b² + c² - 2bc*cosx, подставляем наши переменные:
AC² = AB² + BC² - 2*AB*BC*cosβ, однако угол β - это двойной угол α:
β = 2*α, тогда косинус будет:
cosβ = cos2α = 2cos²α - 1
AC² = AB² + BC² - 2*AB*BC*(2cos²α - 1) - убираем степень и решаем:
AC = √(AB² + BC² - 2*AB*BC*(2cos²α - 1)) = √(10² + 8² - 2*10*8*(2*(-0,5)² - 1)) = √(100 + 64 - 160*(0,25 - 1)) = √(164 - 160*(-0,75)) = √(164 + 120) = √284 = 16,85229... = 16,9 H
|R| = |AC| = 16,9 Н - модуль суммарного вектора.
Направление показано на рисунке: по оси X - в сторону действия силы F2 под углом в 30° к ней, по оси Y - в сторону силы F1 под углом в 30° к ней.