Question

Як робити 3-6 завдання?

Answer 1

Ответ:

Пошаговое объяснение:

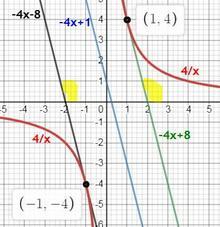
3) график функции у= 4/х

надо, чтобы касательная была ║ графику у = -4х +1

здесь надо отметить, что для параллельности прямых у = ах + b

надо, чтобы их коэффициенты при х были равны

найдем этот коэффициент из уравнения касательной

найдем уравнение касательной в точке х₀

$\displaystyle y_k = y(x_0)+y'(x_0)(x-x_0)$

точку х₀ нам предстоит найти, учитывая, что коэффициент при х в уранении касательной = -4, а из уравнения касательной мы видим, что этот коэффициент будет y'(x₀)

$\displaystyle y'(x) = \bigg ( \frac{4}{x} \bigg )'=-\frac{4}{x^2}; \quad \Rightarrow y(x_0) = -\frac{4}{x^2_0}$

отсюда мы имеем

$\displaystyle -\frac{4}{x^2_0} =-4; \Rightarrow x= \pm 1$

таким образом мы нашли две абсциссы точек, в которых касательные к графику функции у = 4/х будут параллельны прямой у = -4х + 1

тогда найдем и сами точки

у(1) = 4 точка А(1; 4)

у(-1) = -4  точка В(-1; -4)

4) найдем уравнения касательной в каждой из этих точек

х₀ = 1

$\displaystyle y_k_{(1;4)}= \frac{4}{1} -\frac{4}{1^2} (x-1) = 4-4(x-1) = -4x+8$

x₀ = -1

$\displaystyle y_k_{(-1;-4)}= \frac{4}{-1} -\frac{4}{(-1)^2} (x-1) = -4-4(x-1) = -4x-8$

5) тангенс угла находится как производная заданной ф-ции в точке касания

у нас в обеих точках

$\displaystyle tg \alpha = -\frac{4}{x^2_0} =-\frac{4}{1^2} =-\frac{4}{(-1)^2} = -4$

тогда ∠α arctg(-4) ≈ 104°

6) расстояние между точками А(1; 4) и В(-1 ;-4)

$\displaystyle d = \sqrt{(B_x -A_x)^2+(B_y -A_y)^2 }=\sqrt{ (-1 - 1)^2 + (-4 - 4)^2} =\sqrt{68}$

на графике углы наклона касательных обозначу желтым