Предмет: Математика,
автор: Oh1sorry
пример 104, 133, 135 с подробным решением, пожалуйста
Приложения:

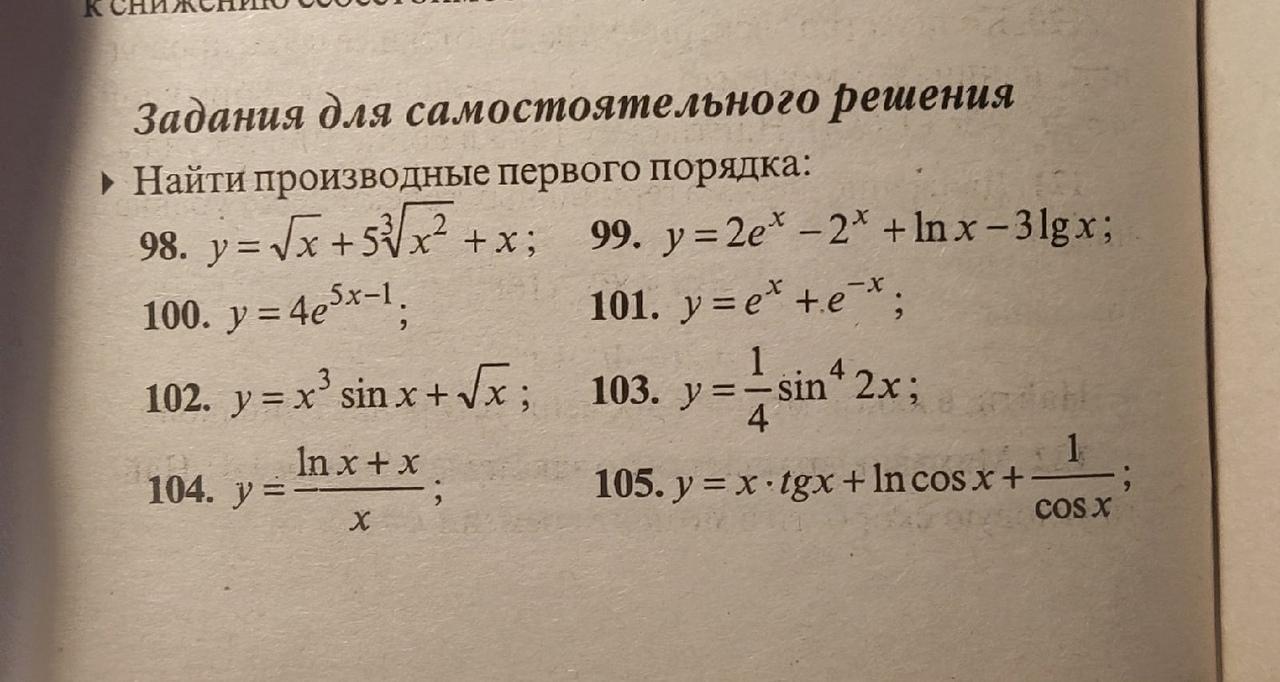
Ответы
Автор ответа:
1
Ответ:
104
133
135
Похожие вопросы
Предмет: Математика,
автор: rogozhnikova20
Предмет: Химия,
автор: roganov11
Предмет: Русский язык,
автор: Аноним
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: Тимур34737284