Question

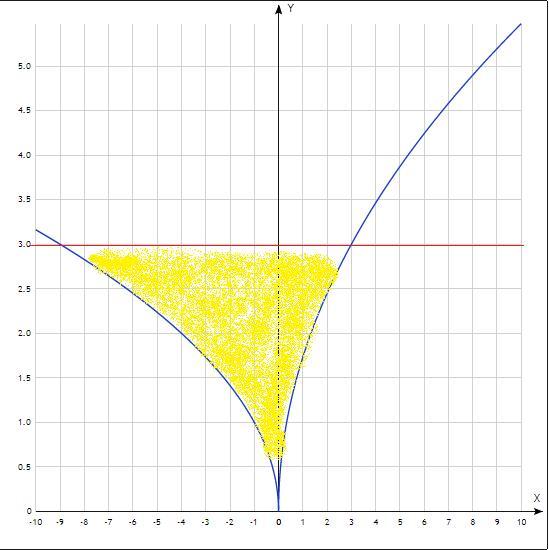
Найти площадь фигуры, ограниченной линиями y=√-x ; y=√3x ; y=3​

Answer 1

проанализируем данные функции

$\displaystyle y_1=\sqrt{-x};\\\\ODZ: x\leq 0\\\\y_2=\sqrt{3x}\\\\ODZ:x\geq 0$

и у=3 прямая.

y₁ и у₂ имеют только одну общую точку при х=0 у=0

найдем точки пересечения у₁ и у₂ с прямой у=3

$\displaystyle\sqrt{-x}=3; -x=9; x=-9\\\\\sqrt{3x}=3; 3x=9;x=3$

тогда площадь фигуры будет образована двумя фигурами справа и слева от оси Оу

$\displaystyle S=\int\limits^0_{-9} (3-\sqrt{-x})\, dx+ \int\limits^3_0 (3-\sqrt{3x})\, dx=\\\\ \bigg(3x-\frac{(-x)^{3/2}*(-1)}{3/2} \bigg)^0_{-9}+ \bigg(3x-\frac{1}{3}* \frac{(3x)^{3/2}}{3/2}\bigg)^3_0=\\\\=0-\bigg(3*(-9)+\frac{2}{3}\sqrt{-(-9)^3}\bigg)+\bigg(3*3-\frac{2}{9}*\sqrt{(3*3)^3}\bigg)=\\\\=-\bigg(-27+\frac{2}{3}*27\bigg)+\bigg(9-\frac{2}{9}*27\bigg)=\\\\=27-18+9-6=12$