Предмет: Математика,
автор: buntmanslava
Помогите пожалуйста решить примеры
Приложения:
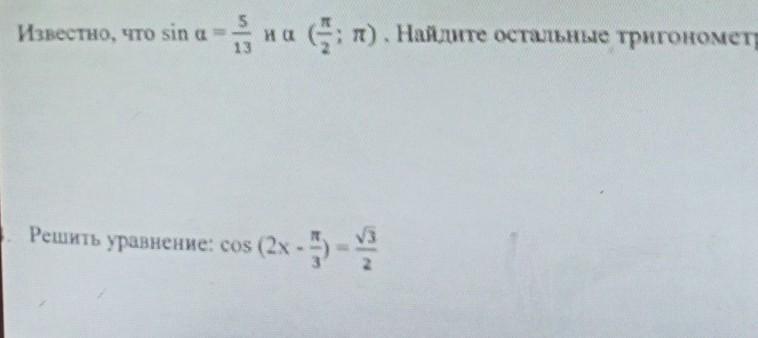
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Приложения:
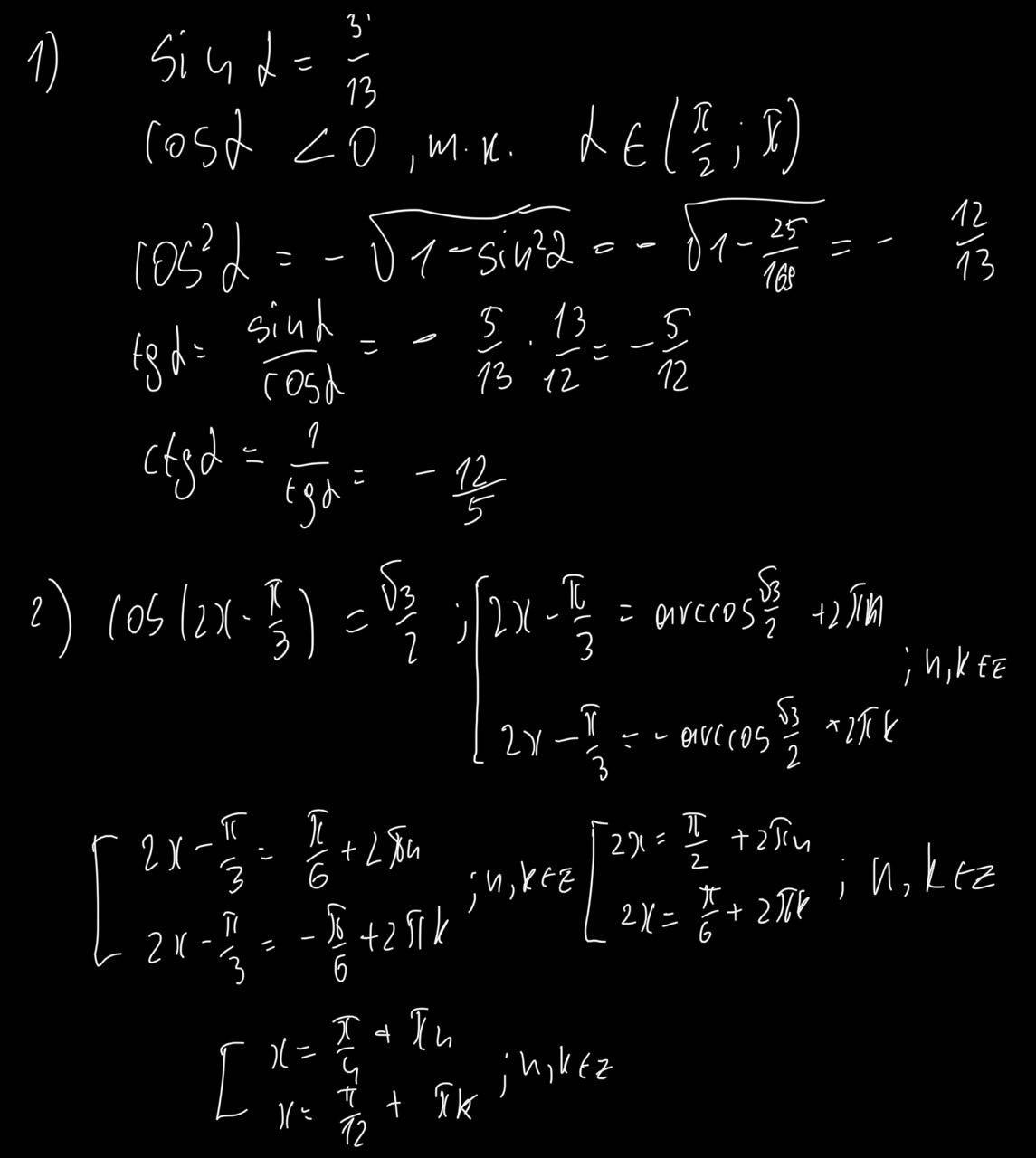
Автор ответа:
0
Ответ:
1.
угол принадлежит 2 четверти, значит косинус, тангенс и котангенс отрицательные.
2.
n принадлежит Z.
Похожие вопросы
Предмет: Математика,
автор: dashapoli
Предмет: Математика,
автор: masudahon
Предмет: География,
автор: arsvereschagin
Предмет: Математика,
автор: MrMarmok22811
Предмет: Английский язык,
автор: умник1702