Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста!!! Номер 7.3, 7.7 с проверкой !!!!!
Приложения:
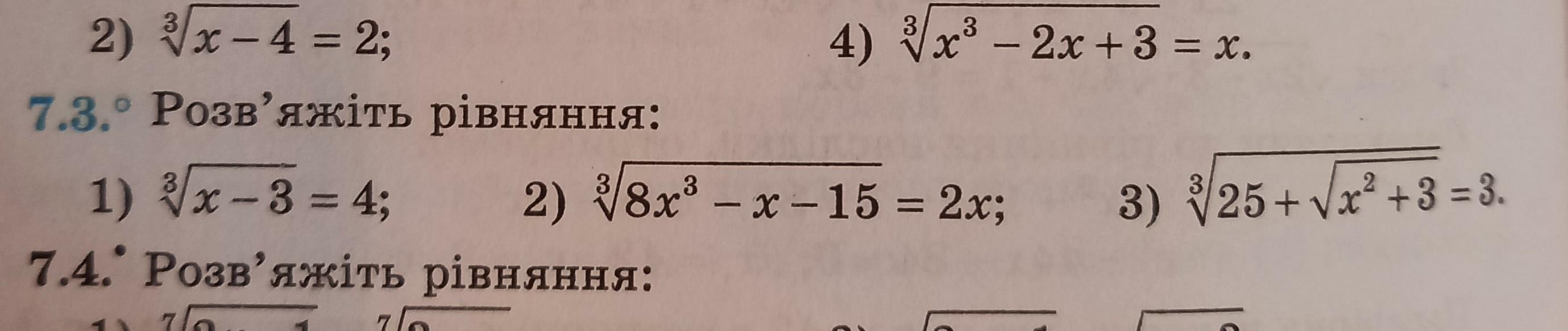
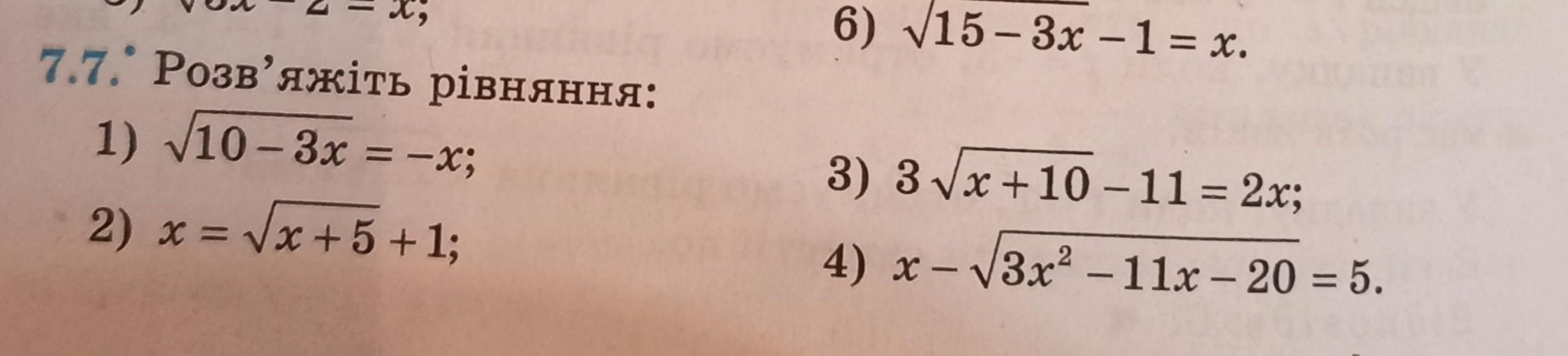
Ответы
Автор ответа:
1
Ответ:
7.3
1
Проверка:
2.
Проверка:
3.
нет корней
7.7
1.
х1 примерно 0,3
х2 примерно -3,3
Проще найти ОДЗ, чем сделать проверку:
х1 не подходит
Ответ:
2.
Проверка:
Ответ: 4
3.
проверка:
х1 = -1
х2 = -31/4
сразу видно, что правая часть < 0, значит не подходит
Ответ: - 1
4.
х1 = 5
х2 = - 9/2
слева отрицательное выражение, не подходит
Ответ: х = 5
Miroslava227:
число 3
Похожие вопросы
Предмет: Математика,
автор: dkoskova97
Предмет: Литература,
автор: Veronica2015
Предмет: Алгебра,
автор: эля981
Предмет: Математика,
автор: Dasna020315