Question

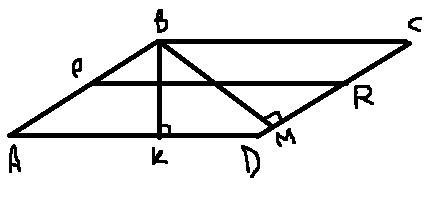
В параллелограмме ABCD угол между высотами ВК и BM равен 45° и AK : KD = 3:2. Найдите площадь параллелограмма, если средняя линия трапеции
KBCD равна 7 мм.​

Answer 1

Ответ:

S=60мм²

Объяснение:

Пусть PR - ср. линия трапеции KBCD. PR=1/2*(KD+BC). Пусть х - 1 часть. Тогда AK=3x, KD=2x, AD=BC.

7=1/2*(2x+5x)

7x=14

x=2

AK=3*2=6мм

AD=5*2=10мм

Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен острому углу параллелограмма.

Значит <BAD=45°. Тогда прямоуг. тр-к △АКВ также будет равнобедренным и АК=ВК

S=BK*AD=6*10=60мм²