Предмет: Математика,
автор: daniillobzanov
привет. помогите пожалуйста ❤
Приложения:
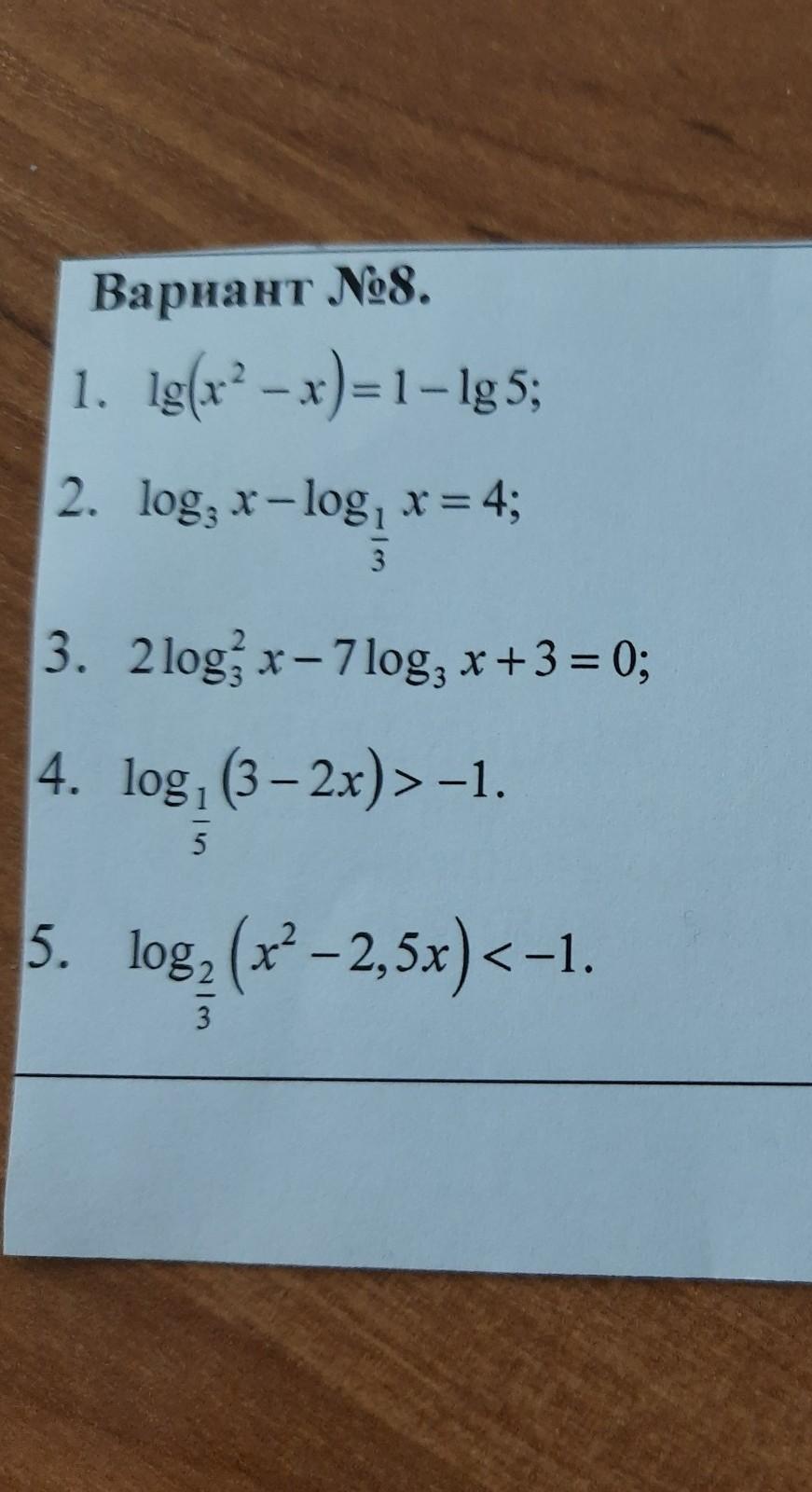
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
1.
2.
3)
4)
5)
теперь проверим этот ответ на область определения функции
x² - x > 0; ⇒ x∈ (-∞; 0) ∪ (1; +∞)
теперь надо объединить два условия и тогда получим ответ
x ∈ (-0.5; 0) ∪ (0; 1)
Похожие вопросы
Предмет: Алгебра,
автор: rinat988
Предмет: Алгебра,
автор: marinatojkieva
Предмет: Химия,
автор: Аноним
Предмет: Информатика,
автор: AgaAgaAAA
Предмет: Українська мова,
автор: Sonyaklep
log1\5 (3-2x) > -1
(1/5)^-1 > 3 - 2x
5 > 3 - 2x
2x > 3 - 5
2x > -2
x > -1