Предмет: Математика,
автор: lee0
здравствуйте, помогите пожалуйста решить задания под номерами 7.16, 1.16, 2.16
Приложения:
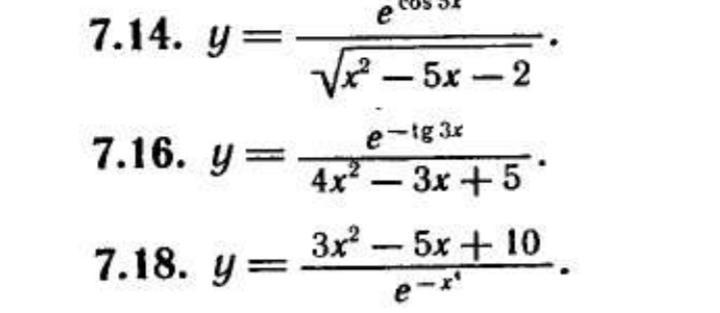

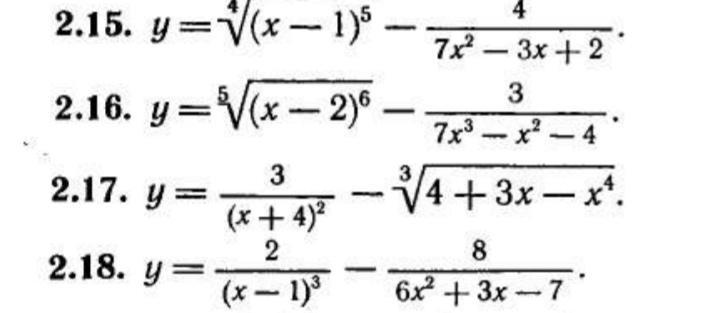
Ответы
Автор ответа:
1
Ответ:
1.16
2.16
7.16
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: asobana
Предмет: Английский язык,
автор: 19lilia
Предмет: География,
автор: elebalenalin
Предмет: Другие предметы,
автор: динара280