Question

Решите, плиз, с рисуночком​

Answer 1

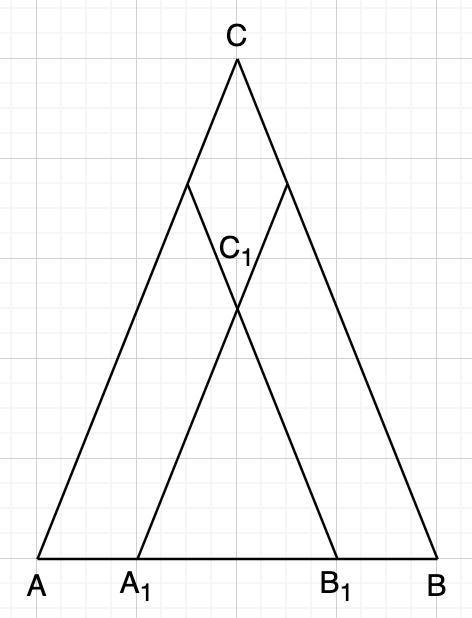
Пусть треугольник ABC -- равнобедренный с основанием AB. Выберем точку C₁ внутри треугольника ABC и проведем через нее прямые A₁C₁ || AC и B₁C₁ || BC.

Углы CAB и C₁A₁B₁ являются соответственными углами, образованными при пересечении параллельных прямых A₁C₁ и AC секущей AB, поэтому ∠CAB = ∠C₁A₁B₁.

Углы CBA и C₁B₁A₁ являются соответственными углами, образованными при пересечении параллельных прямых B₁C₁ и BC секущей AB, поэтому ∠CBA = ∠C₁B₁A₁.

Треугольник ABC является равнобедренным, прилежащие к основанию AB углы равны: ∠CAB = ∠CBA. Но тогда также выполняется равенство ∠C₁A₁B₁ = ∠C₁B₁A₁. Из этого следует, что треугольник A₁B₁C₁ является равнобедренным с основанием A₁B₁.

Равенство углов ACB и A₁C₁B₁ следует из равенства остальных углов двух треугольников:

∠ACB = 180° – (∠CAB + ∠CBA) = 180° – (∠C₁A₁B₁ + ∠C₁B₁A₁) = ∠A₁C₁B₁.

Answer 2

Объяснение:

дано:

∆ABC - равнобедренный

доказать:

∆A1B1C1 - равнобедренный

А = A1

B = B1

C = C1

доказательство:

так как по условию AB = A1B1; BC = B1C1

треугольник A1B1C1 подобен ABC.

так как углы при основании равны, A = A1, B = B1. значит и C = C1