Question

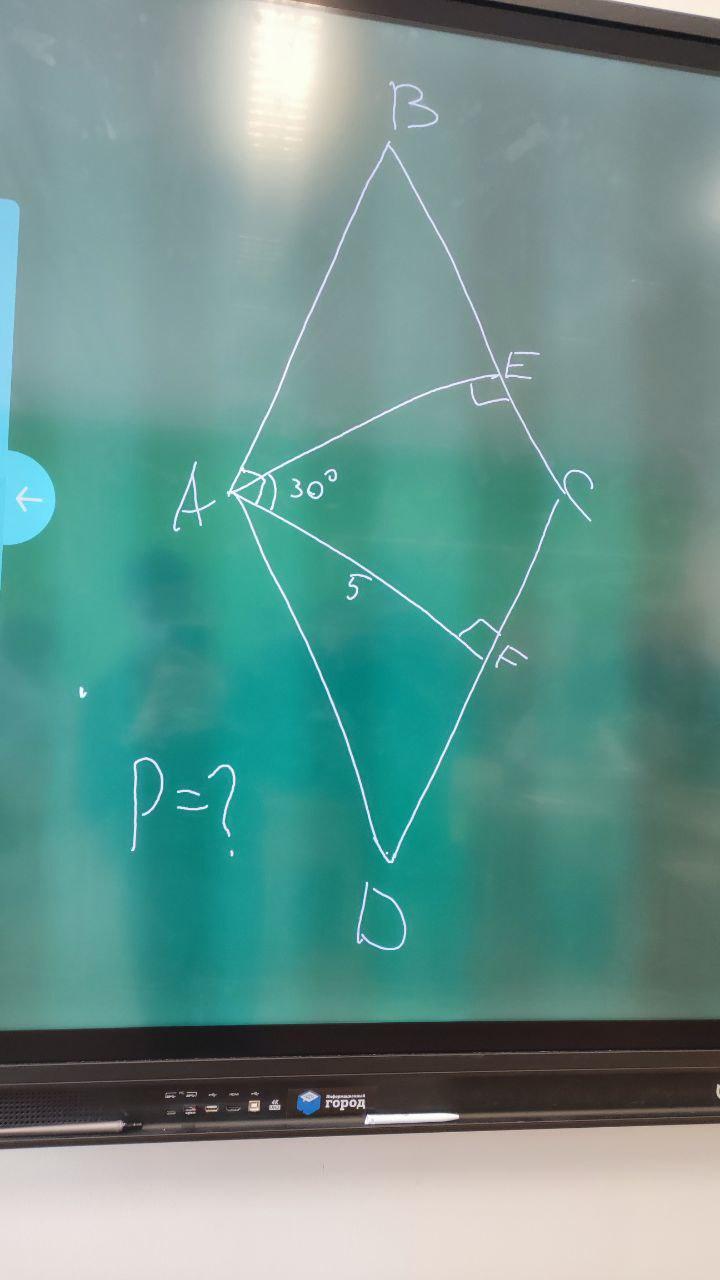
Решите задачу. Угол между высотами ромба, проведенными из одной из его вершин, равен 30°. Высота ромба равна 5 см. Найдите периметр ромба.

Answer 1

Для ясности сделаем обозначения.

Ромб - АВСД.

Высоты АК и АЕ.

Угол ЕАК = 30°.

АК = 5см.

Решение:

так как АЕ -высота, она образует со стороной ДС угол 90°.

Но и со стороной АВ//ДС она тоже образует угол ЕАВ = 90°.

Тогда угол ВАК = угол ЕАВ - угол ЕАК = 90° - 30° = 60°.

Тр-к АВК прямоугольный, так как АК - высота.

Значит угол АВК = 90° - угол ВАК = 90°-60°=30°.

А катет АК, лежащий против угла АВК = 30°, равен половине гипотенузы АВ, то есть АВ = 2АК = 10 (см)

Периметр ромба Р = 4а = 4 · 10 = 40 (см)