Question

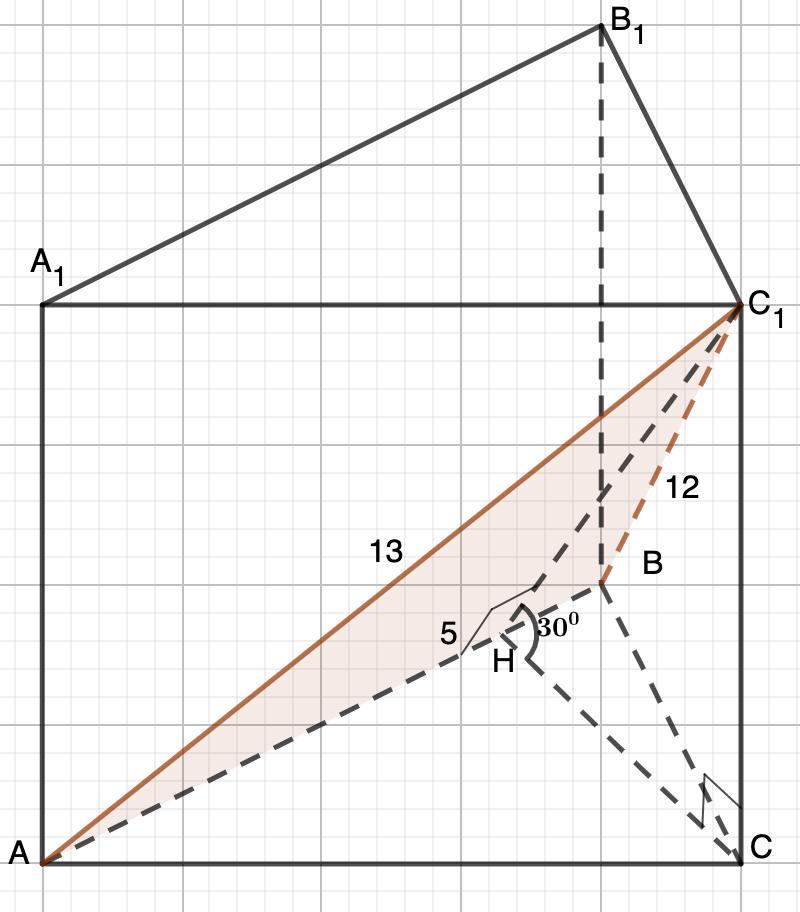
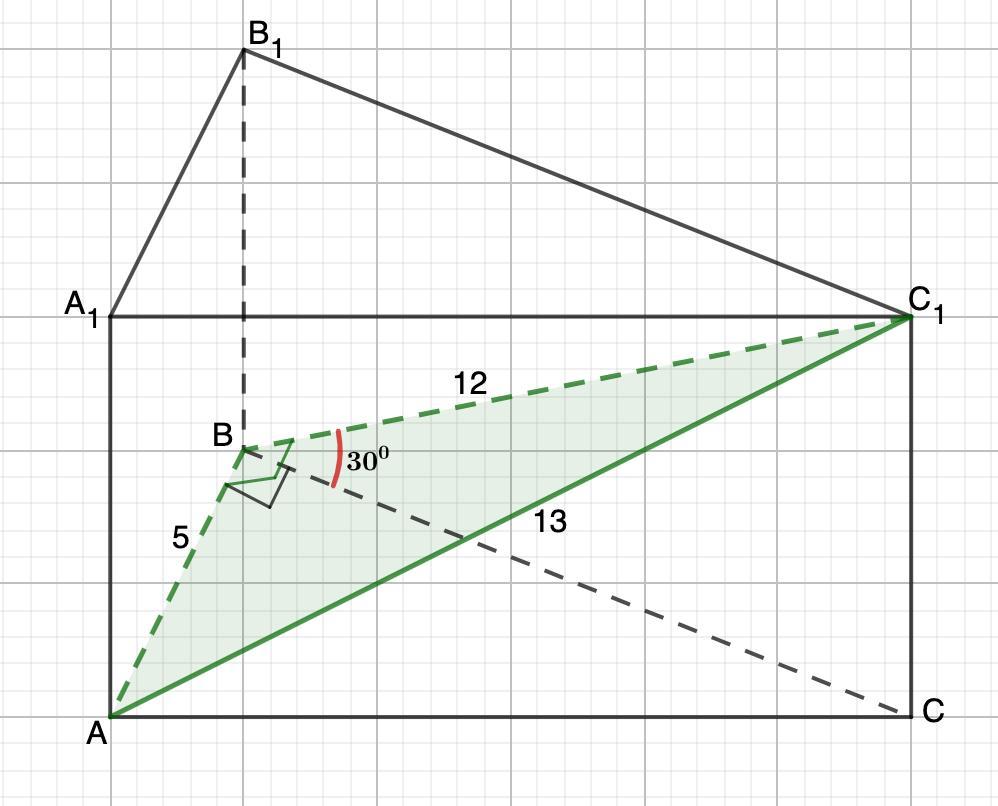
сечением прямой треугольной призмы плоскостью проведённой через ребро нижнего основания длина которого равна 5 и вершину верхнего основания является треугольник со сторонами 5 12 и 13. Найдите объем призмы, если известно, что угол между плоскостью данного сечения и нижним основанием равен 30°.

Answer 1

Ответ:

$90\sqrt{3}$ см³

Пошаговое объяснение:

Дано: Прямая треугольная призма АВСА₁В₁С₁;

Сечение - ΔАВС₁: АВ=5 см; АС₁=13 см, ВС₁=12 см.

∠С₁НС=30°

Найти: $V_{ABCA_1B_1C_1}$

Решение:

1. Найдем площадь сечения по формуле Герона:

$S=\sqrt{p(p-a)(p-b)(p-c)}$, где р-полупериметр; a,b,c - стороны треугольника.

р=(5+12+13):2=15 (см)

$S_{ABC_1}=\sqrt{15(15-5)(15-12)(15-13)}=\sqrt{15*10*3*2}=\sqrt{3*5*2*5*3*2}=3*5*2=30\; (_{CM^2})$

С другой стороны, площадь треугольника равна:

$S_{ABC_1}=\frac{1}{2} AB*HC_1$

$\displaystyle 30=\frac{5}{2} *HC_1$

$HC_1=30:\frac{5}{2}=30*\frac{2}{5} =12$ (см)

2. Рассмотрим ΔСНС₁ - прямоугольный.

∠С₁НС=30°

⇒ $CC_1=\frac{1}{2}HC_1$ (как катет, лежащий против угла 30°)

$CC_1=12:2=6$ (см)

По теореме Пифагора найдем НС:

$HC=\sqrt{HC_1^2-CC_1^2}=\sqrt{12^2-6^2}=\sqrt{108}=6\sqrt{3}$ (см)

3. Найдем площадь основания:

$S_{ABC}=\frac{1}{2}AB*HC=\frac{1}{2}*5*6\sqrt{3}=15\sqrt{3}$ (см²)

4. Найдем объем призмы:

$V=S_{OCH}*h$

$V_{ABCA_1B_1C_1}=S_{ABC}*CC_1=15\sqrt{3}*6=90\sqrt{3}$ (см³)

* В результате вычислений мы получили, что С₁Н=С₁В=12 см ⇒ΔАВС₁ прямоугольный. Но на ответ это не влияет.

Выше приведено общее решение задачи.

Попробуем внимательней рассмотреть данные задачи.

1. Стороны треугольного сечения равны 5, 12 и 13. То есть:

13²=5²+12² или 169=144+25

⇒ ΔАВС₁ - прямоугольный (т. Пифагора)

⇒ ∠С₁ВС = 30°

2. Рассмотрим ΔСВС₁ - прямоугольный (призма прямая)

$CC_1=\frac{1}{2}BC_1=12:2=6$ (катет, лежащий против угла 30°)

По теореме Пифагора:

$BC=\sqrt{BC_1^2-CC_1^2}=\sqrt{144-36}=\sqrt{108}=6\sqrt{3}$

3. С₁В⊥АВ (п.1)  ⇒СВ⊥АВ (теорема о трех перпендикулярах)

4. Рассмотрим ΔАВС - прямоугольный (п.3)

$S_{ABC}=\frac{1}{2}*AB*BC=\frac{1}{2}*5*6\sqrt{3}=15\sqrt{3}$

5. Найдем объем призмы:

$V_{ABCA_1B_1C_1}=S_{ABC}*CC_1=15\sqrt{3}*6=90\sqrt{3}$  (ед²)