Question

Решите задачу по Геометрии ​

Answer 1

Ответ:

Доказательство в объяснении.

Объяснение:

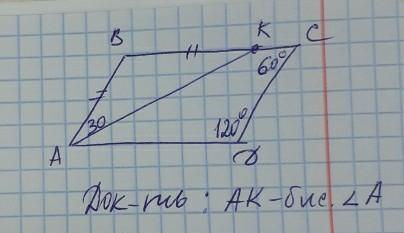
Так как внутренние односторонние углы ∠BCD и ∠ADC при прямых AD и ВС и секущей DC в сумме равны  

60° + 120° = 180°, то прямые AD и ВС параллельны по признаку.

Треугольник АВК равнобедренный и углы при основании равны. => ∠BАК и ∠ВКА  = 30°.

∠BКА и ∠КAD - внутренние накрест лежащие при параллельных прямых AD и ВС и секущей АК, следовательно,  ∠BКА = ∠КAD = 30°.  

Итак, ∠BАК = ∠КAD = 30°. Следовательно, АК - биссектриса угла BAD, что и требовалось доказать.

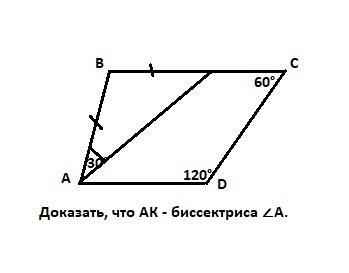
P.S. Четырехугольник ABCD по условию не параллелограмм (cм. приложение №2).