Предмет: Алгебра,
автор: mariast91027
СРОЧНО! Помогите пожалуйста решить определенный интеграл (13)
Приложения:
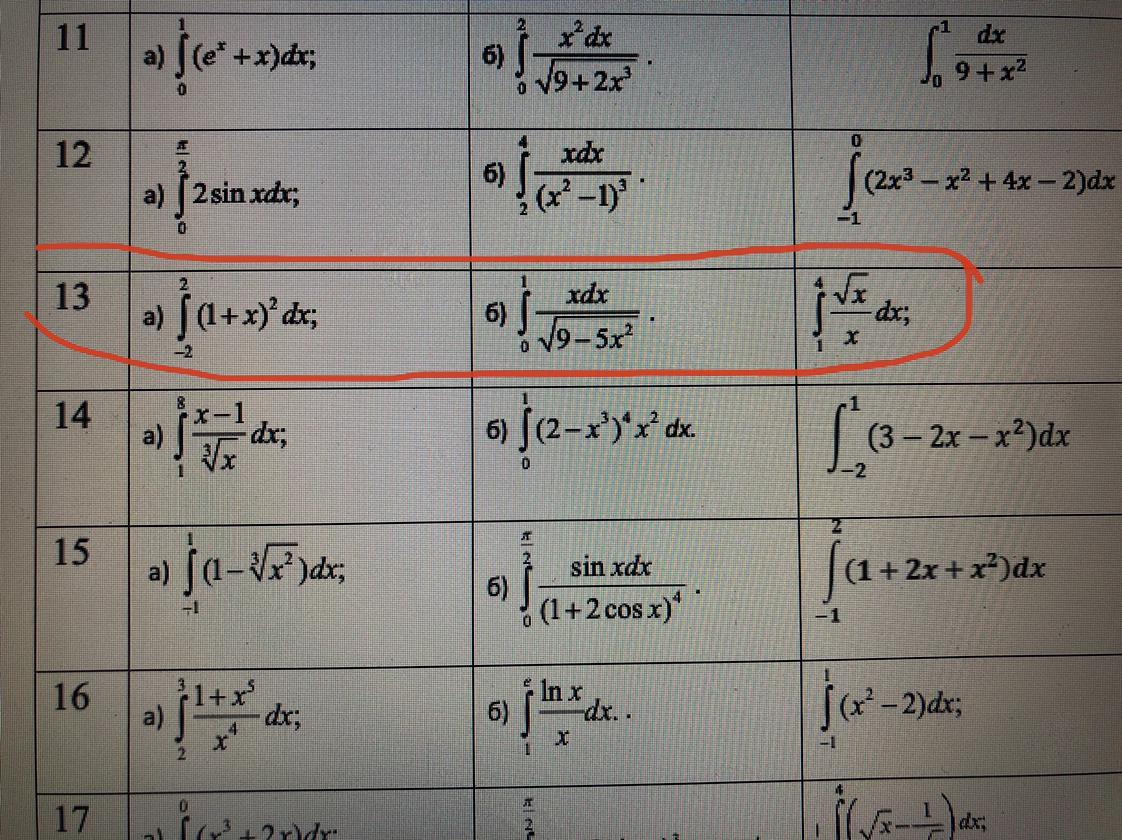
Ответы
Автор ответа:
2
Отметьте пожалуйста лучшим решением и поставьте сердечко
Приложения:

Автор ответа:
2
Ответ:
а)
б)
в)
Похожие вопросы
Предмет: Химия,
автор: ksenagomzokova
Предмет: Биология,
автор: химия5
Предмет: Алгебра,
автор: dashakorotkova1
Предмет: Английский язык,
автор: botanya2005
Предмет: Алгебра,
автор: Fakla