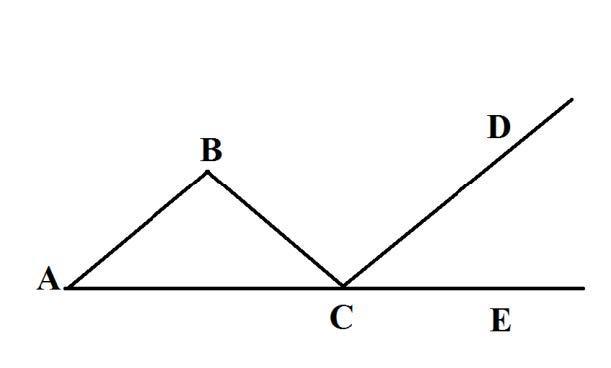
На рисунке AB=BC, угол А=30 градусов
угол DCE = 1/5 угла BCE
Докажите, что AB ||CD
Ответы
Ответ:
Так как, по условию, АВ = ВС, то треугольник АВС равнобедренный, тогда угол ВСА = ВАС = 600.
Тогда угол АВС = (180 – ВАС – ВСА) = (180 – 60 – 60) = 600, а следовательно треугольник АВС равносторонний, АВ = ВС = АС.
Рассмотрим треугольник АСД у которого угол САД = 600, а угол АСД = АСВ / 2 = 60 / 2 = 300, так как СД биссектриса угла АСВ.
Тогда угол АДС = (180 – АСД – САД) = (180 – 30 – 60) = 900.
Следовательно, АВ перпендикулярно СД, что и требовалось доказать.
Объяснение:
<А=30
АВ=ВС
<DCE=1/5<BCE
Доказать:АВ||СD
Треугольник АВС - ранобедренный
<С=<А=30
<АСВ и <ВСЕ смежные
Сумма смежных углов равен 180
<ВСЕ=180-<АСВ=180-30=150
<DCE=1/5<BCE=1/5×150=30
<BAC=<DCE=30как соответственные. Соответственные углы равны значит прямaя
АВ||СD. Что и требовалось доказать