Предмет: Математика,
автор: evgenia98745688
Производная функция
Приложения:
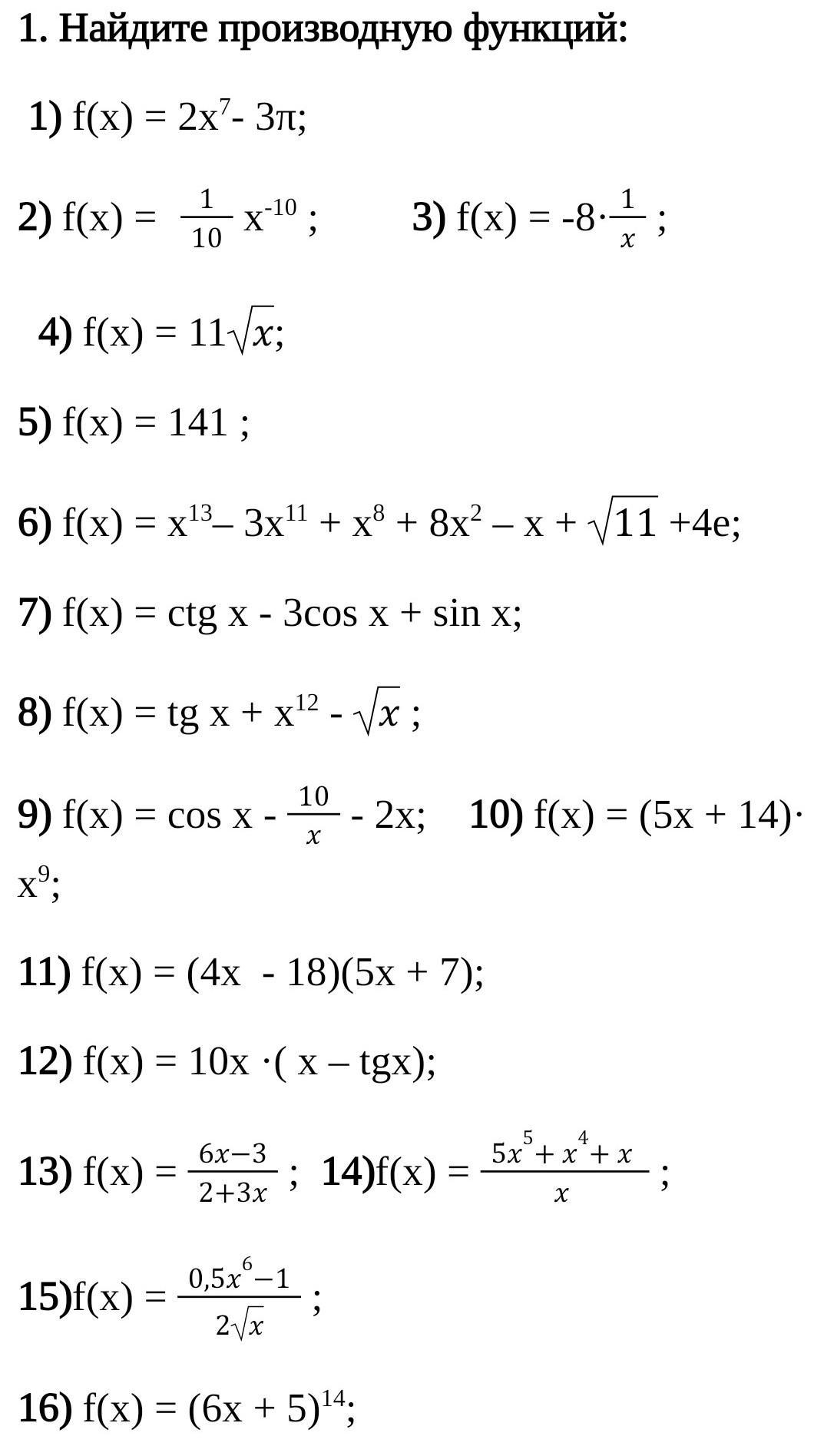
Ответы
Автор ответа:
0
Ответ:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Похожие вопросы
Предмет: Алгебра,
автор: olesya5496
Предмет: Русский язык,
автор: Аннет11
Предмет: Алгебра,
автор: nrf27
Предмет: Немецкий язык,
автор: dfrederiko
Предмет: Русский язык,
автор: алиса838