Предмет: Математика,
автор: evgenia98745688
производная функция помогите пожалуйста
Приложения:
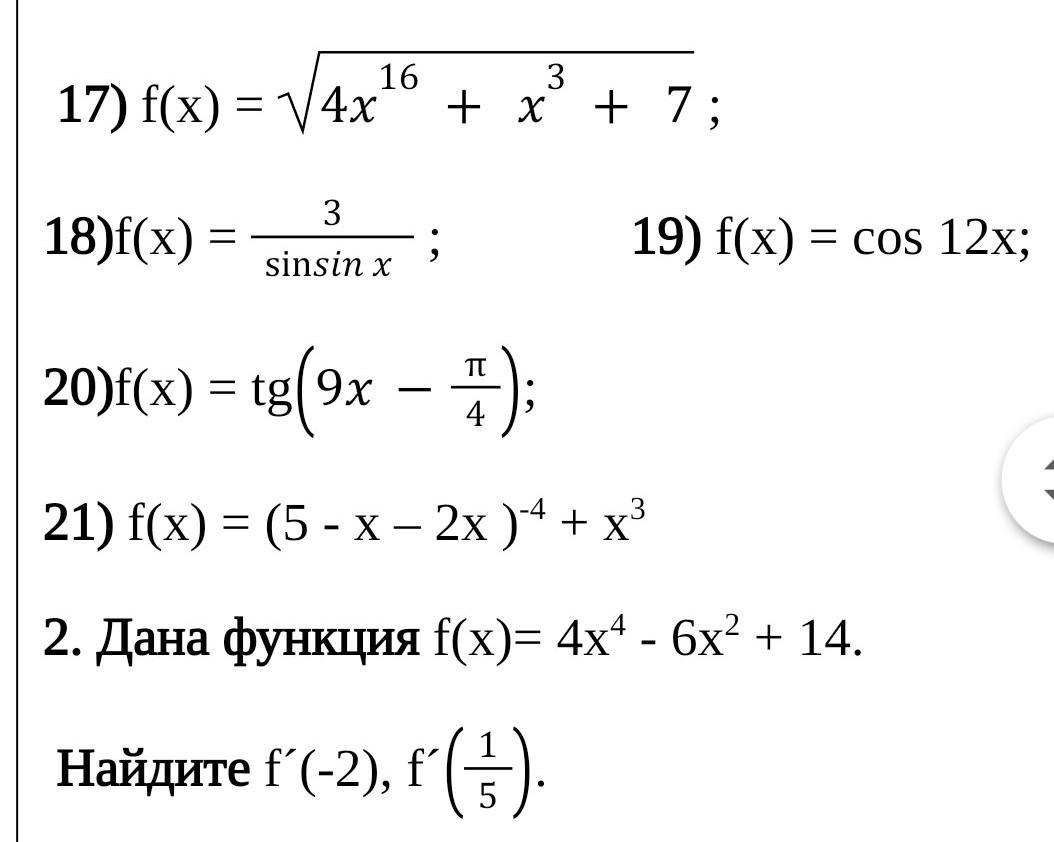
Ответы
Автор ответа:
1
Ответ:
17
18
19
20
21
2.
evgenia98745688:
спасибо большое
можешь ещё помочь, если не трудно
не понимаю эту тему
Похожие вопросы
Предмет: Химия,
автор: zzz26
Предмет: Химия,
автор: kotsoeva
Предмет: Беларуская мова,
автор: DiMiK181
Предмет: Литература,
автор: ZakhaR37
Предмет: Математика,
автор: гуся5