Предмет: Математика,
автор: floris7
вычислить площадь фигур ограниченных линиями:y²+2y+1=3x, 3x-3y=7
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
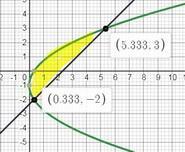
y²+2y+1=3x это парабола ветвями вправо
3x-3y=7 прямая
найдем точки пересечения (по у)
второе подставим в первое и получим у₁ = -2; у₂=3
тогда наша площадь будет считаться по формуле
Приложения:
Похожие вопросы
Предмет: Химия,
автор: Twiger
Предмет: Математика,
автор: PolinaSteshenko
Предмет: Русский язык,
автор: katwrina
Предмет: Русский язык,
автор: cherepkovi