Предмет: Алгебра,
автор: DembelNick
Помогите решить: Sinx + 2cosx = |Sinx|
Ответы
Автор ответа:
0
1) sinx>=0 sinx+2cosx=sinx 2cosx=0
cosx=0 sinx>=0
x=П/2+2Пk
2)sinx<0
sinx+2cosx=-sinx
sinx+cosx=0
cos(П/2-x)+cosx=0
2cosП/4cos(П/4-x)=0
cos(П/4-x)=0
П/4-x=П/2+Пk
x=-П/4+Пk sinx<0
x=-П/4+2Пk
cosx=0 sinx>=0
x=П/2+2Пk
2)sinx<0
sinx+2cosx=-sinx
sinx+cosx=0
cos(П/2-x)+cosx=0
2cosП/4cos(П/4-x)=0
cos(П/4-x)=0
П/4-x=П/2+Пk
x=-П/4+Пk sinx<0
x=-П/4+2Пk
Автор ответа:
0
2)sinx+cosx=0
sinx+sin(π/2-x)=0
2sinπ/4cos(π/4-x)=0
cos(π/4-x)=0
π/4-x=π/2+πn
x=-π/4+πn
Такой же ответ. Нет никакой ошибки!
sinx+sin(π/2-x)=0
2sinπ/4cos(π/4-x)=0
cos(π/4-x)=0
π/4-x=π/2+πn
x=-π/4+πn
Такой же ответ. Нет никакой ошибки!
Приложения:
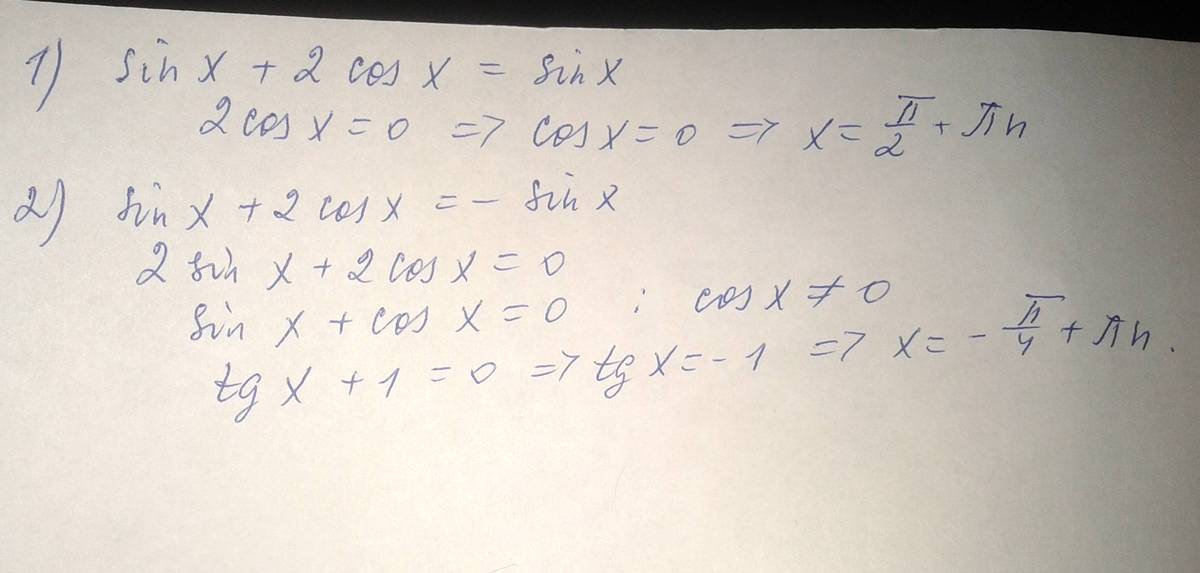
Похожие вопросы
Предмет: Русский язык,
автор: vivakisa
Предмет: Биология,
автор: alisakoltashina36
Предмет: Литература,
автор: dema226
Предмет: Химия,
автор: Dzuliy