Предмет: Геометрия,
автор: sekator
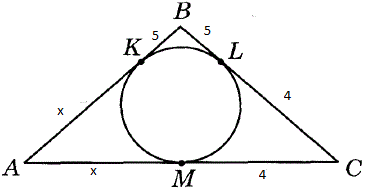
В треугольник ABC вписана окружность, точки касания делят CB на отрезки 4 и 5, считая от вершины C. Угол A = arcsin3/5. Определите площадь треугольника ABC.
Ответы
Автор ответа:
0
Так как арксинус угла а 3/5, то угол А острый и его синус равен 3/5.
Воспользуемся свойством касательной: отрезки касательных к окружности, проведённые из одной точки, равны (BL=BK=5, CL=CM=4, AM=AK=x).
Найдем косинус угла А:

Берем cosA=4/5 так как угол А острый.
Потеореме косинусов:
ВС²=АВ²+АС²-2АВ*АС*cosA
81=(x+5)²+(x+4)²-2*(4/5)(x+5)(x+4)
После возведения в квадрат и приведения подобных получим
x²+9x-180=0
D=81+720=801=3√89
x1=-(9/2)+(3/2)√89
x2=-(9/2)-(3/2)√89<0 - не рассматриваем
S=1/2*AC*AB*sinA



Воспользуемся свойством касательной: отрезки касательных к окружности, проведённые из одной точки, равны (BL=BK=5, CL=CM=4, AM=AK=x).
Найдем косинус угла А:
Берем cosA=4/5 так как угол А острый.
Потеореме косинусов:
ВС²=АВ²+АС²-2АВ*АС*cosA
81=(x+5)²+(x+4)²-2*(4/5)(x+5)(x+4)
После возведения в квадрат и приведения подобных получим
x²+9x-180=0
D=81+720=801=3√89
x1=-(9/2)+(3/2)√89
x2=-(9/2)-(3/2)√89<0 - не рассматриваем
S=1/2*AC*AB*sinA
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: gavrilovasveta804
Предмет: История,
автор: Аноним
Предмет: Қазақ тiлi,
автор: babaevaradina86
Предмет: Литература,
автор: Katya290799