Предмет: Геометрия,
автор: mrvasilenko2000
Решите пж дам 20 баллов
Приложения:

Ответы
Автор ответа:
0
Ответ:
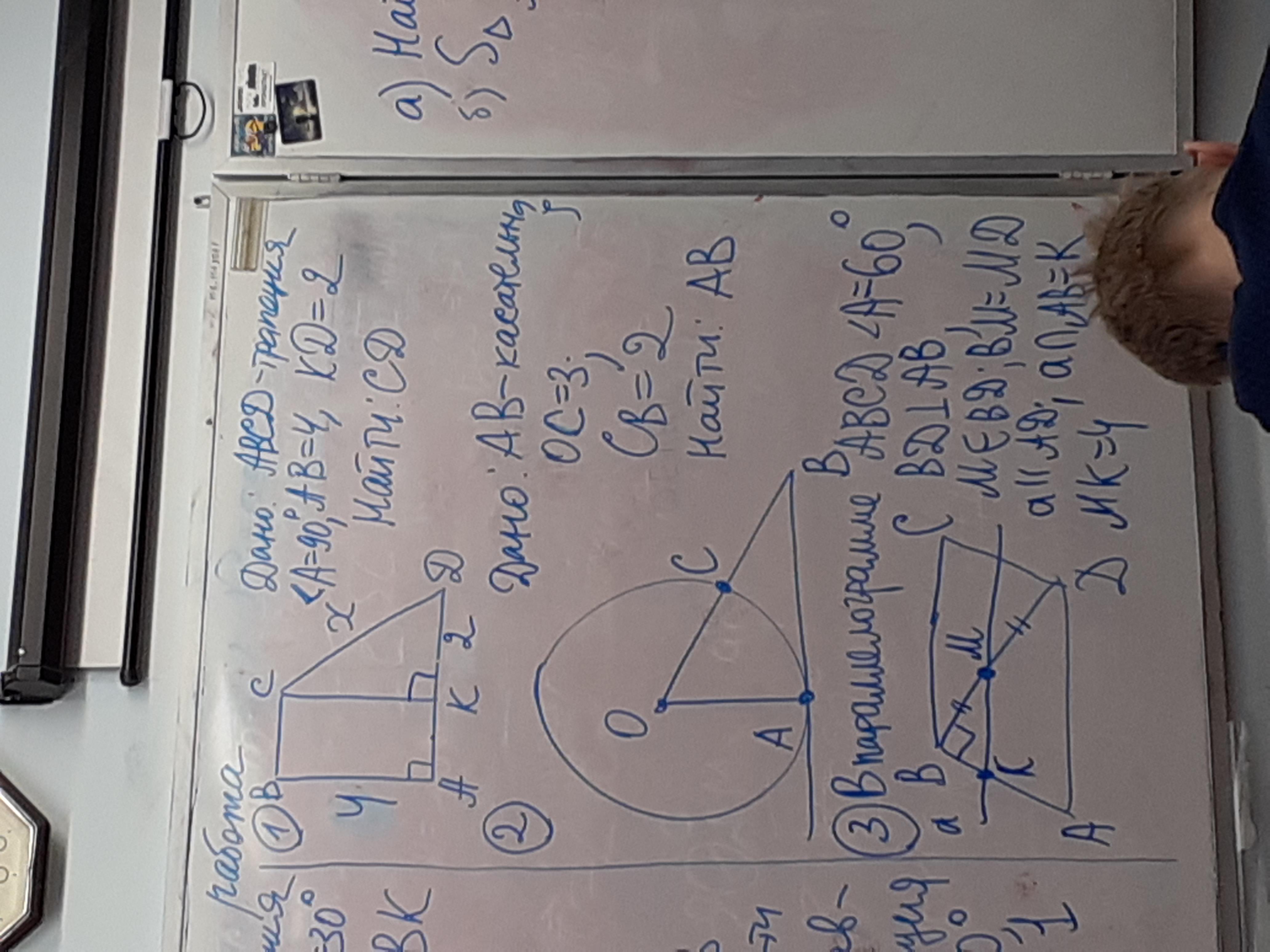
Задачка №1:
- AB = CK = 4, в ΔCKD найдем CD по теореме Пифагора:
Задачка №2:
- По теореме Пифагора найдем
Задачка №3:
- КМ - средняя линия в ΔABD ⇒ AD = 2KM = 8;
- В ΔABD AB = AD/2, так как лежит напротив угла 30°;
- Найдем площадь параллелограмма ⇒
- Из ΔABD найдем BD по теореме Пифагора ⇒
- Опустим из т.М высоту МТ на основание AD
- В ΔМTD найдем МТ, MT = MD/2 (напротив 30°) = BD/4 = √3
- Найдем площадь ΔAMD ⇒
Похожие вопросы
Предмет: История,
автор: stepankozlovicTvist
Предмет: Химия,
автор: ekbOo
Предмет: Русский язык,
автор: natali7791
Предмет: Қазақ тiлi,
автор: мама599
Предмет: Математика,
автор: zulu51