Предмет: Алгебра,
автор: XAEA169
Помогите пожалуйста решить уравнение интегралов
Приложения:
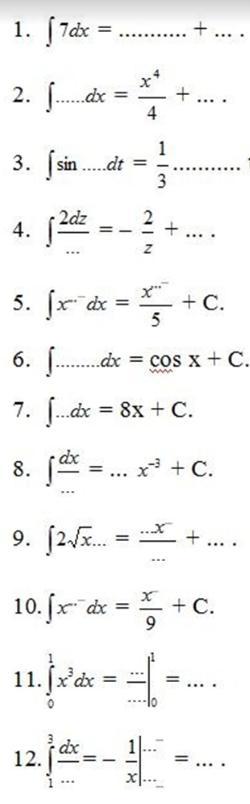
Ответы
Автор ответа:
0
Ответ:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Похожие вопросы
Предмет: Английский язык,
автор: Lera122006
Предмет: Алгебра,
автор: pylyi
Предмет: Химия,
автор: samal25
Предмет: Геометрия,
автор: landsh1
Предмет: Алгебра,
автор: веселюндя