Предмет: Алгебра,
автор: W0lviT
ПОМОГИТЕ С ТЕСТОМ ПО АЛГЕБРЕ СРОЧНО!!!!!!!!!!!!!!!
Приложения:
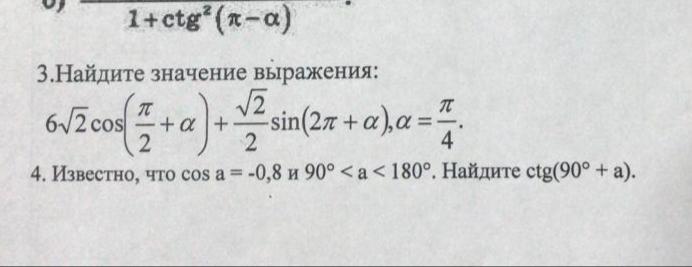
Ответы
Автор ответа:
0
Ответ:
3.
4.
угол принадлежит 2 четверти, синус положительный
Похожие вопросы
Предмет: Математика,
автор: apelsin4ik777
Предмет: География,
автор: danu991199
Предмет: Алгебра,
автор: kiryuha17
Предмет: Алгебра,
автор: Yulia20000
Предмет: Химия,
автор: kva58