Предмет: Математика,
автор: rajjs
помогите пожалуйста
Приложения:
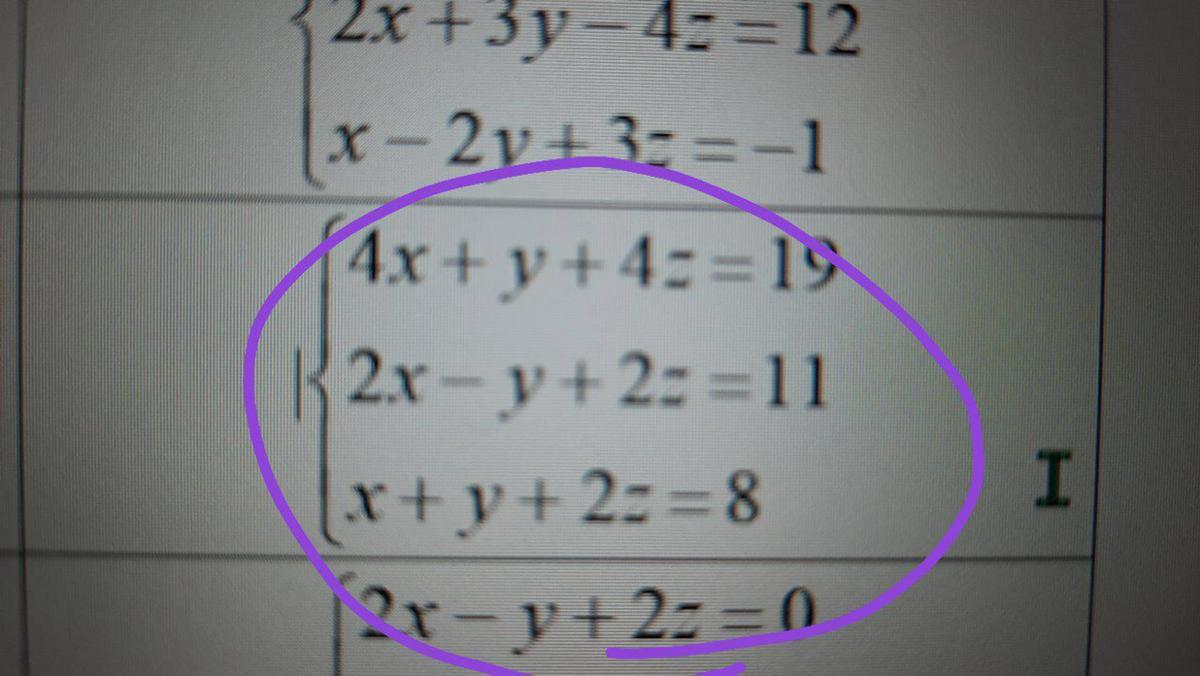
Ответы
Автор ответа:
1
Ответ:
x = 1; y = -1; z = 4
Пошаговое объяснение:
Перепишем систему в матричном виде и решим ее методом Крамера:
Найдем соответствующие определители матриц:
Найдем значения x,y,z:
Похожие вопросы
Предмет: Алгебра,
автор: Freakazoid
Предмет: Математика,
автор: Аайй
Предмет: Русский язык,
автор: dosik32
Предмет: Информатика,
автор: ValyaDyacenko1
Предмет: Алгебра,
автор: Madik199