Question

помогите пожалуйста, отдам все баллы, которые у меня есть, только качественно и пошагово!!​

Answer 1

Ответ:

Пошаговое объяснение:

вариант 1

1. здесь при замене переменной поменяются и пределы интегрирования

в)

$\displaystyle \int\limits^8_1 {\frac{1}{2\sqrt{x+1} } } \, dx =\left[\begin{array}{ccc}u=x+1; \quad du=dx\\ u_{up}=1+8=9 \hfill\\u_{low}=1+1=2 \hfill;\end{array}\right] =\frac{1}{2} \int\limits^9_2{\frac{1}{\sqrt{u} } } \, du =\sqrt{u} \bigg \vert_2^9= 3-\sqrt{2}$

г)

$\displaystyle \int\limits^{32}_1 {x^{-3/2}} \, dx =\frac{5x^{2/3}}{3} \bigg \vert_1^{32}=\frac{5-32^{2/5}}{2} -\frac{5*1^{ 2/5}}{2} =\frac{15}{2}$

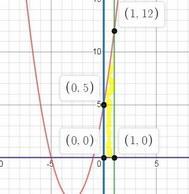
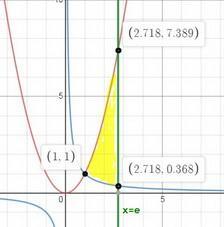
2. чертим график и оттуда берем всё необходимое

$\displaystyle S=\int\limits^1_0 {(x^2+6x+5)} \, dx =\frac{x^3}{3} \bigg \vert_0^1+6\frac{x^2}{2} \bigg \vert_0^1+5x\bigg \vert_0^1=\frac{1}{3} +3+5=\frac{25}{3}$

вариант 3

1.

а)

$\displaystyle \int\limits^3_1 {(x^2-\frac{1}{x^2}) } \, dx =\frac{x^3}{3} \bigg \vert_1^3+\frac{1}{x} \bigg \vert_1^3=\frac{26}{3} -\frac{2}{3} =8$

б)

$\displaystyle \int\limits^{\pi /2}_{\pi /6}21cos \bigg (x-\frac{\pi }{6} } \bigg )\, dx =\left[\begin{array}{ccc}u=x-\pi /6\\\\du=dx \hfill\end{array}\right] =\int\limits^{\pi /2}_{\pi /6}21cosu\, du =21sinu \bigg \vert_{\pi /6}^{ \pi /2}=$

$\displaystyle =21sin(x-\frac{\pi }{6} )\bigg \vert_{\pi /6}^{\pi /2}=21(sin(\pi /3)-sin0)=21\frac{\sqrt{3} }{2}$

в)

$\displaystyle \int\limits^4_2 {e^{0.5x-3}} \, dx =\left[\begin{array}{ccc}u=0.5x-3\\\\du=0.5x\end{array}\right] =2\int\limits^4_2 {e^u} \, du =\\=2e^u\bigg \vert_2^4=2e^{0.5x-3}\bigg \vert_2^4=2(e^{-1}-e^{-2})$

г)

$\displaystyle \int\limits^8_1 {(x^{2/3}+1)} \, dx = \frac{3}{5} x^{5/3}\bigg \vert_1^8+x\bigg \vert_1^8=\frac{93}{5} +7=\frac{128}{5}$

2.

$\displaystyle S=\int\limits^e_1 {(x^2-\frac{1}{x} )} \, dx =\frac{x^3}{3} \bigg \vert_1^e-lnx\bigg \vert_1^e=\frac{e^3-1}{3} -1=\frac{e^3-4}{3}$