Предмет: Алгебра,
автор: Акинатор
рекуррентная последовательность
Приложения:
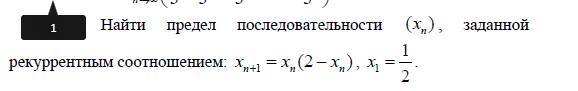
Ответы
Автор ответа:
0
Для начала поймем, как себя ведет последовательность.
1. Если , то
, то 
2. Для любых справедливо
справедливо 
Итак, последовательность возрастает и ограничена, тогда она сходится. Обозначим искомый предел через x. Тогда, переходя к пределу в рекуррентном соотношении, получаем уравнение на х:

В процессе решения уравнения было учтено, что x>1/2, поэтому можно безбоязненно сокращать на x.
Предел последовательности равен 1.
1. Если
2. Для любых
Итак, последовательность возрастает и ограничена, тогда она сходится. Обозначим искомый предел через x. Тогда, переходя к пределу в рекуррентном соотношении, получаем уравнение на х:
В процессе решения уравнения было учтено, что x>1/2, поэтому можно безбоязненно сокращать на x.
Предел последовательности равен 1.
Похожие вопросы
Предмет: Физика,
автор: pashakorzhov
Предмет: Химия,
автор: fanerka47
Предмет: Математика,
автор: ivanushtakov2009
Предмет: Математика,
автор: Андрей33
Предмет: История,
автор: 2600510