Таблица 9.2 первый признак подобия треугольников
Ответы
Ответ:
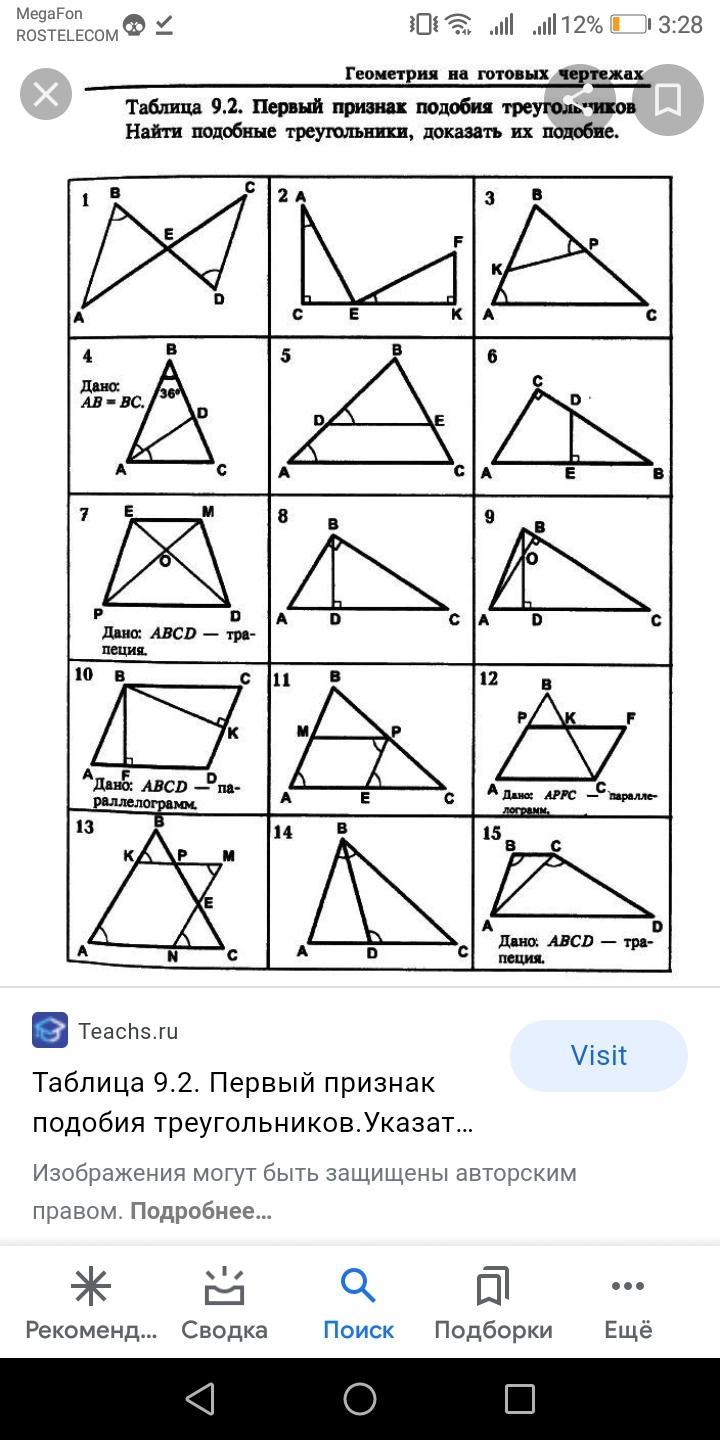
Таблица 9.2. Первый признак подобия треугольников.
Первый признак подобия треугольников:
- если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
1. ΔABE ~ ΔCDE, так как
∠B = ∠D, а углы при вершине Е равны, как вертикальные.
2. ΔACE ~ ΔEKF, так как
∠С = ∠К = 90° и ∠А = ∠Е
3. ΔВРК ~ ΔВАС, так как
∠Р = ∠А, ∠В - общий.
4. АВ = ВС, треугольник АВС равнобедренный, значит углы при основании равны.
- Сумма углов треугольника равна 180°.
∠ВАС = ∠ВСА = (180° - 36°) / 2 = 144° / 2 = 72°
∠DAC = 0,5∠BAC = 0,5 · 72° = 36°
Из ΔADC:
∠ADC = 180° - (∠DAC + ∠DCA) = 180° - (36° + 72°) = 180° - 108° = 72°
ΔADC ~ ΔBAC
5. ΔDBE ~ ΔABC, так как
∠D = ∠А, а ∠B - общий.
6. ΔАВС ~ ΔDBE, так как
∠АСВ = ∠DEB = 90°, а ∠В - общий.
7. ЕМ║PD как основания трапеции.
∠ОМЕ = ∠OPD как накрест лежащие при пересечении ЕМ║PD секущей РМ,
∠ЕОМ = ∠DOP как вертикальные, значит
ΔЕОМ ~ ΔDOP.
8. Сумма острых углов прямоугольного треугольника равна 90°.
Из ΔАВС: ∠А = 90° - ∠С
Из ΔBDC: ∠DBC = 90° - ∠C, значит
∠А = ∠DBC.
А так как и ∠АВС = ∠BDC = 90°, то
ΔАВD ~ ΔBCD.
ΔАВС ~ ΔADB, так как
∠А общий, а ∠AВС = ∠ADB = 90°.
ΔABC ~ ΔBDC, так как
∠С - общий, а ∠АВС = ∠BDC = 90°.
9. ΔABC ~ ΔKDC, так как
∠С - общий, а ∠АВС = ∠KDC = 90°.
10. ΔABF ~ ΔCBK, так как
∠А = ∠С как противолежащие углы параллелограмма,
∠AFB = ∠CKB = 90°.
11. ∠МРЕ = ∠СЕР, а эти углы - внутренние накрест лежащие при пересечении прямых МР и АС секущей РЕ, значит
МР║АС.
ΔВМР ~ ΔВАС, так как
∠ВМР = ∠ВАС как соответственные при МР║АС и секущей АВ, а ∠В - общий.
ΔРЕС ~ ΔВАС, так как
∠РЕС = ∠ВАС, а ∠С - общий.
Из подобия этих треугольников следует, что ∠В = ∠ЕРС.
ΔРЕС ~ ΔВМР, так как
∠РЕС = ∠ВМР (∠РЕС = ∠ВАС, а в свою очередь ∠ВАС = ∠ВМР),
∠В = ∠ЕРС.
12. ΔВРК ~ ΔВАС, так как
∠В - общий, ∠ВРК = ∠ВАС как соответственные при PF║AC, и секущей АВ. (PF║AC как противолежащие стороны параллелограмма).
ΔВРК ~ ΔCFK, так как
∠ВРК = ∠CFK (∠ВРК = ∠ВАС, а ∠ВАС = ∠CFK как противолежащие углы параллелограмма),
углы при вершине К равны как вертикальные.
ΔВАС ~ ΔCFK, так как
∠ВАС = ∠CFK и ∠ВСА = ∠FKC как накрест лежащие при PF║AC, и секущей КС.
13. ΔВАС ~ ΔВКР, так как
∠ВАС = ∠ВКР и ∠В - общий.
ΔВАС ~ ΔENC, так как
∠ВАС = ∠ENC, а ∠С - общий.
Из подобия следует, что ∠АВС = ∠NEC.
ΔВКР ~ ΔENC, так как
∠АВС = ∠NEC и ∠ВКР = ∠ENC.
ΔENC ~ ΔEMP, так как
∠ENC = ∠EMP и углы при вершине Е равны как вертикальные.
ΔВКР ~ ΔEМР, так как
∠ВКР = ∠EМР и углы при вершине Р равны как вертикальные.
ΔВАС ~ ΔЕМР, так как
∠ВАС = ∠ЕМР и ∠АВС = ∠МЕР.
14. ΔАВС ~ ΔBDC, так как
∠ABC = ∠BDC и ∠С - общий.
15. ВС║AD как основания трапеции, АС - секущая, тогда
∠ВСА = ∠DAC как накрест лежащие.
А так как по условию ∠АВС = ∠DCA, то
ΔАВС ~ ΔDCA.
