Question

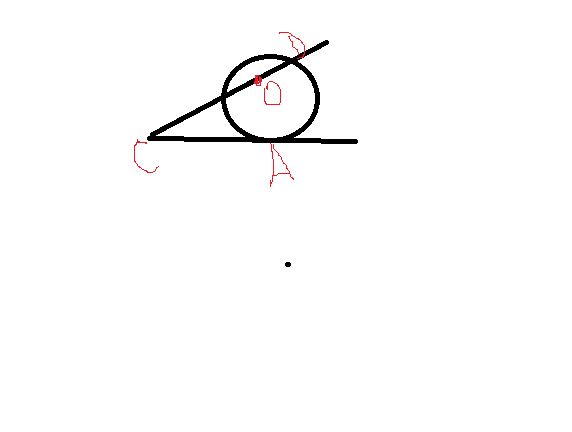
угол ACO равен 10 градусов. Его сторона CA касается окружности.Найдите градусную величину большей дуги AD окружности, заключенной внутри этого угла.

Answer 1

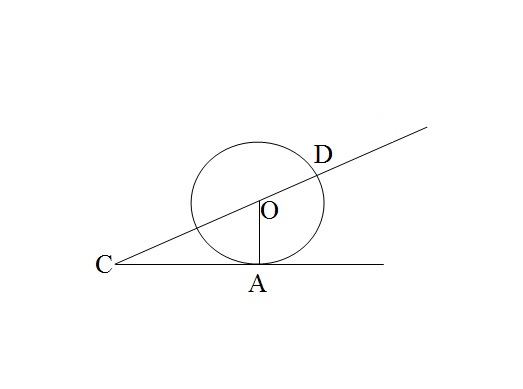
Как я поняла, т.О-центр окружности.

Проведем из центра окружности прямую к касательной(ОА-радиус).
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Следовательно, угол САО=90 градусов.

Рассмотри треугольник САО-прямоугольный.
Угол А=90, угол С=10, следовательно, угол О=180-(90+10)=80 градусов.

Углы СОА и DOA смежные. Сумма смежных углов равна 180 градусам.
Угол DOA=180-80=100.
Величина центрального угла равна величине дуги, на которую опирается.
Дуга AD равна 100 градусам.