Question

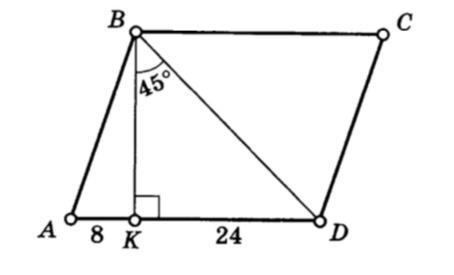
найдите площадь параллелограмма

Answer 1

Ответ:

используя теорему синусов найдем ВD

$\frac{bd}{ \sin(90) } = \frac{24}{ \sin(45) } \\ \frac{bd}{1} = \frac{24}{ \frac{ \sqrt{2} }{2} } \\ bd = 24 \sqrt{2}$

используя теорему Пифагора найдем BK

${bd}^{2} = {bk}^{2} + {kd}^{2} \\ (24 \sqrt{2} ) ^{2} = {bk}^{2} + 24 ^{2} \\ {bk}^{2} = 576 \times 2 - 576 \\ bk ^{2} = 576 \\ bk = 24$

найдем площадь ABK

$s = \frac{ah}{2} \\ s = \frac{8 \times 24}{2} = 96$

найдем площадь KBD

$s = \frac{24 \times 24}{2} = \frac{576}{2} = 288$

площадь паралелограмма состоит из илощади авк и вкд умноженный на 2

$s = 2 \times (96 + 288) = 2 \times 384 = 768$

ответ 768

Answer 2

Ответ:

S=768

Объяснение:

∆ВКD- прямоугольный,равнобедренный треугольник (<ВКD=90°; <KBD=45°; <BDK=45°) BK=KD

BK=24

АD=AK+KD=8+24=32

S=AD*BK=32*24=768