Предмет: Алгебра,
автор: cinkalina
Упростите выражение и найдите его значение
очень срочно, помогите пожалуйста
Приложения:
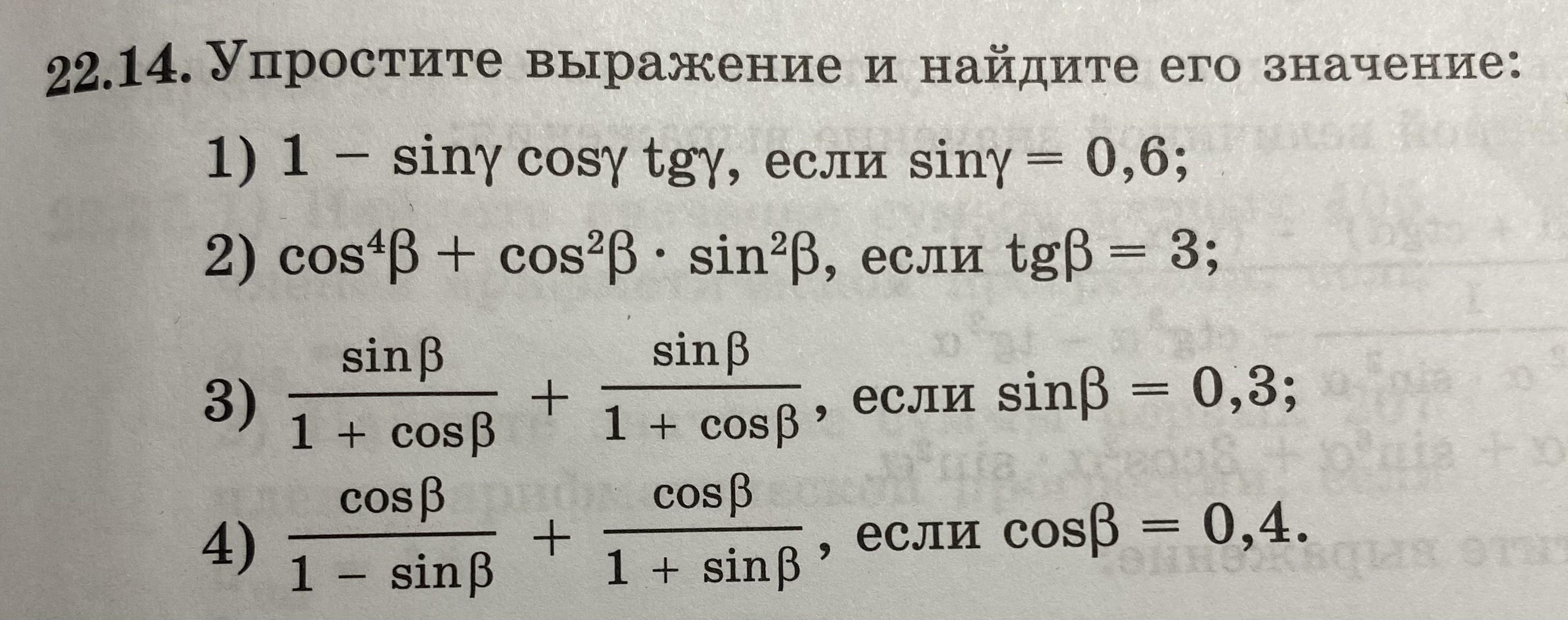
Universalka:
В третьем задании опечатка. В знаменателе первой дроби должен быть минус, а не плюс .
Ответы
Автор ответа:
1
1 и 4 точно правильно
Приложения:

Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: www50
Предмет: Алгебра,
автор: Кисюлька201
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Clique88
Предмет: Другие предметы,
автор: Кот007004