Предмет: Геометрия,
автор: Ilyaa342
Даю 15 баллов.
Радиусы оснований усеченного конуса равны 8 см и 5 см, а его образующая наклонена к плоскости основания под углом 45 градусов. Вычислить объем усеченного конуса.
Ответы
Автор ответа:
8
Ответ: 129π см3
Объяснение:
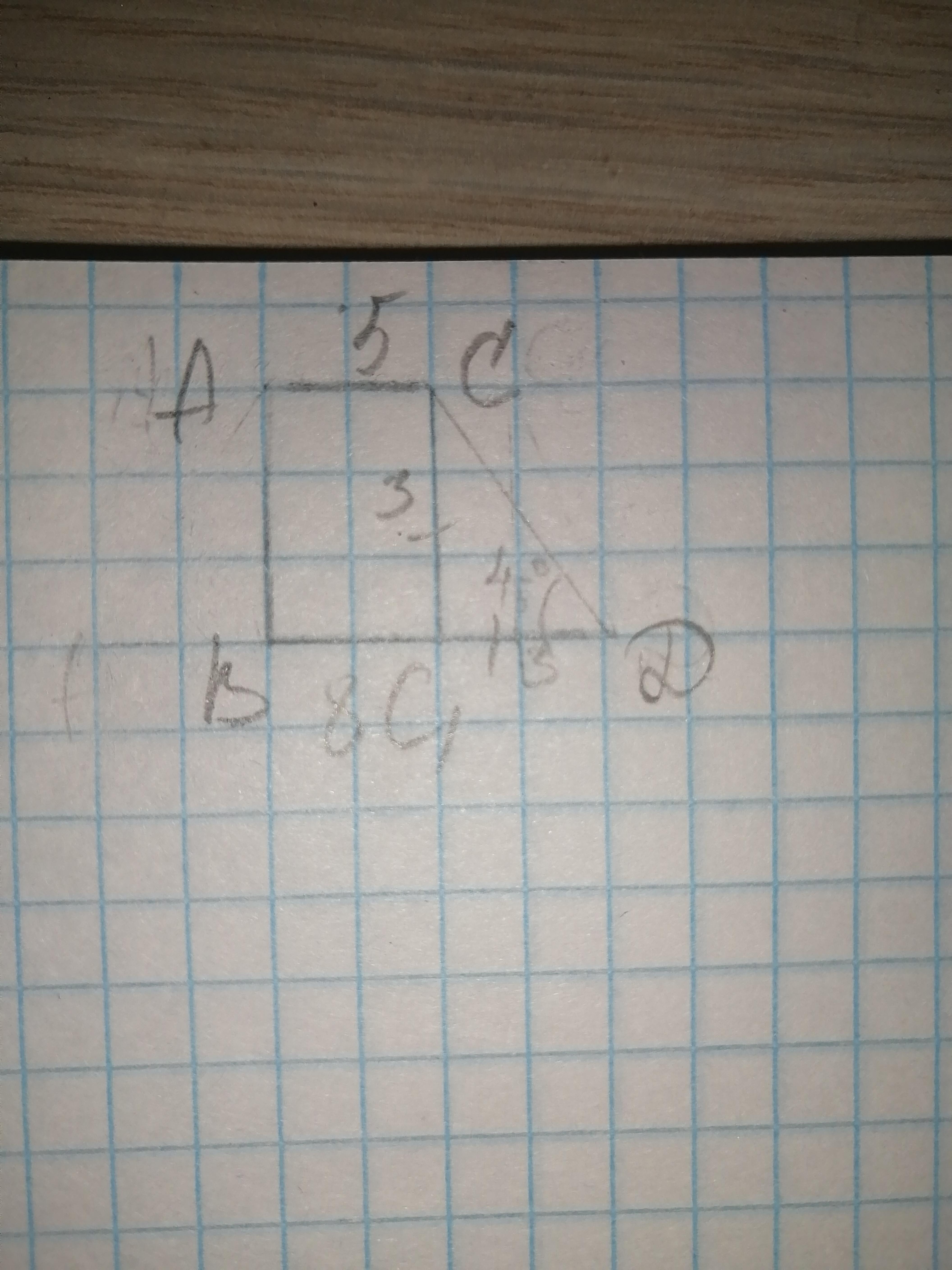
Так как образующая наклонена под углом 45 градусов, а треугольник прямоугольный, то есть сумма всех его углов равна 180 градусам, второй угол тоже будет 45 градусов и значит, что треугольник дан равнобедренный
Чтобы найти сторону C1D, мы отнимем от 8 5 и получится 3
Теперь можно найти образующюю по теореме Пифагора:
√3^2+3^2=3√2
Далее подставляем все значения в формулу:
V ус.к.=1/3*π*h(r1+r1*r2+r2)=1/3*π*3(8^2+8*5+5^2)=129π см3
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Samole
Предмет: Физика,
автор: GrIgOrY01
Предмет: Русский язык,
автор: azkasky
Предмет: Қазақ тiлi,
автор: kuwoh
Предмет: Русский язык,
автор: айгуль236