Предмет: Геометрия,
автор: xadson2
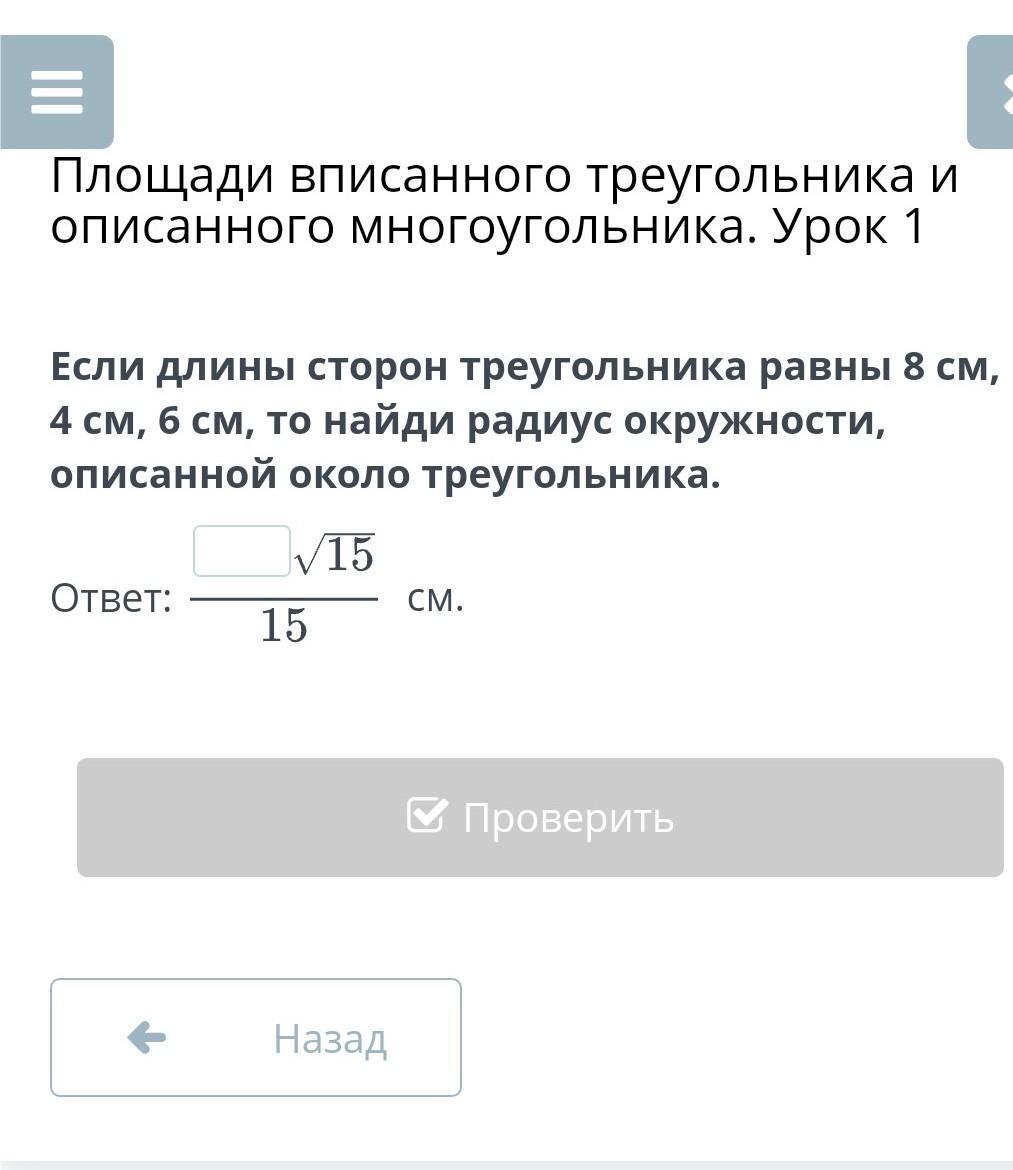
Если длины сторон треугольника равны 8 см, 4 см, 6 см, то найди радиус окружности, описанной около треугольника.
Помогите даю 50 баллов пожалуйста
Приложения:
Ответы
Автор ответа:
1
Ответ:
Объяснение:
1 способ.
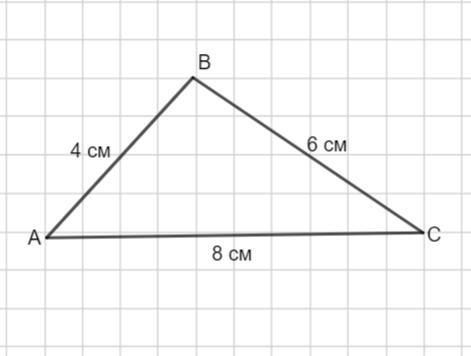
Рассмотрим треугольник ABC.
AB=4 см,BC=6 см, AC=8 см.
Найдем площадь треугольника по формуле Герона.
где стороны треугольника.
см.
Тогда найдем площадь.
см²
Радиус окружности, описанной около треугольника найдем по формуле.
см.
2 способ.
Найдем косинус угла В.
По теореме косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Найдем синус угла В. Воспользуемся основным тригонометрическим тождеством.
Найдем радиус окружности, описанной около треугольника по формуле:
где α - угол, лежащий напротив стороны а.
Приложения:
Похожие вопросы
Предмет: История,
автор: skromnyaschka
Предмет: Физика,
автор: ррр24
Предмет: Математика,
автор: tysiabarnayl
Предмет: Математика,
автор: Софушкка
Предмет: Геометрия,
автор: luizd1