Question

Сумма углов треугольника. Внешний угол треугольника. Урок 4
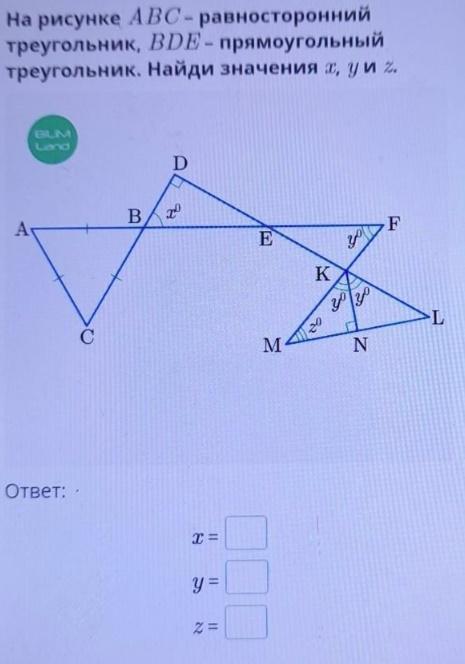
На рисунке ABC – равносторонний треугольник, BDE – прямоугольный треугольник. Найди значения x, y и z.

Ответ:
x =
y =
z =

помогите пожалуйста решить срочно нужны ответы!!!!!!!!!!!!!!!!!!!!!!!¡!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!​

Answer 1

Ответ:

х = 60°

у = 50°

z = 40°

Объяснение:

1) ΔАВС-равносторонний.  Все углы равностороннего треугольника равны между собою и составляют 60°. ∠АВС = 60°

∠DBE = ∠АВС = 60° - как вертикальные.

х = ∠DBE = 60°

2) Δ BDE – прямоугольный. ∠D=90°. ∠DBE = 60°.

Так как сумма острых углов прямоугольного треугольника равна 90°, то ∠DEВ = 90°-60°=30°

∠FEK=∠DEВ=30° - как вертикальные.

∠EFK=y

Так как сумма углов треугольника равна 180°, то:

∠FKE = 180°-∠FEK-∠EFK=180°-30°-y=150°-y

∠МКL = ∠MKN+∠LKN=y+y=2y

∠FKE=∠МКL - как вертикальные, поэтому:

150°-y = 2у

3у=150

у = 50°

3) KN - высота ΔМКL, так как ∠MKN = ∠LKN, то KN - биссектриса.

Если в треугольнике высота, проведенная к основанию, совпадает с биссектрисой, то треугольник равнобедренный.

В равнобедренном треугольнике углы при основании равны.

∠М=∠L=(180°-∠МКL)÷2=(180°-2*50°)÷2=40°

z = ∠М = 40°