Question

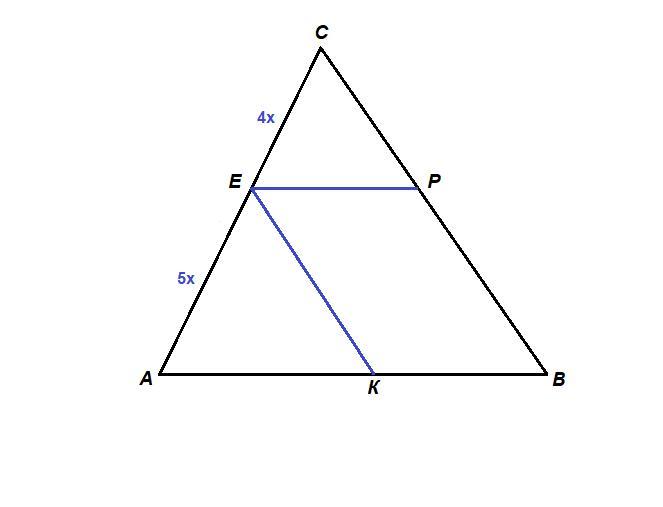
В треугольнике ABC через точку E , которая делит сторону AC в отношении 5:4 , считая от вершины A , проведены прямые, параллельные AB и BC . Прямая, параллельная AB , пересекает BC в точке P , а параллельная BC пересекает AB в точке K . Известно, что AB=45

Найдите длину отрезка AK.

Найдите длину отрезка PE .

Найдите отношение BP:PC . Ответ выразите в виде конечной десятичной дроби.

Answer 1

Ответ:

AK = 25

PE = 20

$\dfrac{BP}{PC}=1,25$

Объяснение:

Обобщенная теорема Фалеса:

• параллельные прямые отсекают на сторонах угла пропорциональные отрезки.

∠ВАС,  ЕК║ВС, тогда верно отношение:

$\dfrac{AE}{AC}=\dfrac{AK}{AB}$

$\dfrac{AE}{AC}=\dfrac{AE}{AE+EC}=\dfrac{5}{9}$

$\dfrac{AK}{AB}=\dfrac{5}{9}$

$\boldsymbol{AK}=\dfrac{5\cdot AB}{9}=\dfrac{5\cdot 45}{9}\boldsymbol{=25}$

KB = AB - AK = 45 - 25 = 20

ЕРВК - параллелограмм, так как его противолежащие стороны параллельны.

РЕ = КВ = 20 как противолежащие стороны параллелограмма.

∠АСВ, ЕР║АВ, по обобщенной теореме Фалеса:

$\boldsymbol{\dfrac{BP}{PC}}=\dfrac{AE}{EC}=\dfrac{5}{4}\boldsymbol{=1,25}$