Помогите решить, и дам 50! баллов.
Ответы
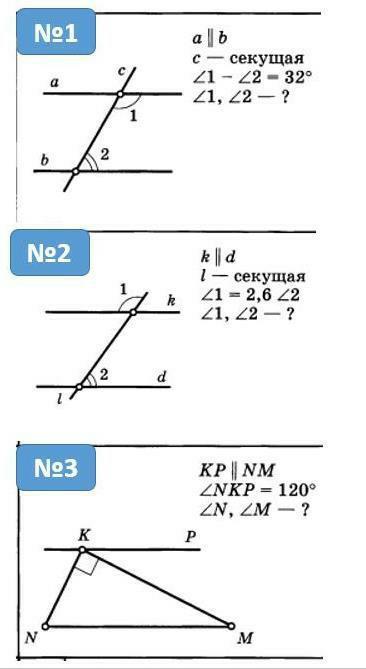
Задание №1.
Дано :
a || b, с — секущая.
∡1 - ∡2 = 32°.
Найти :
∡1 = ?
∡2 = ?
Решение :
- При пересечении двух параллельных прямых секущей сумма внутренних односторонних углов равна 180°.
Следовательно, ∡1 + ∡2 = 180°.
Составим систему уравнений —
∡1 + ∡2 = 180°
∡1 - ∡2 = 32°.
Складываем их —
∡1 + ∡2 + ∡1 - ∡2 = 180° + 32°
2×∡1 = 212° | : 2
∡1 = 106°.
Вернёмся в первое уравнение системы, подставим туда значение ∡1 и узнаем значение ∡2 —
∡1 + ∡2 = 180°
∡2 = 180° - ∡1 = 180° - 106° = 74°.
Ответ :
∡1 = 106°, ∡2 = 74°.
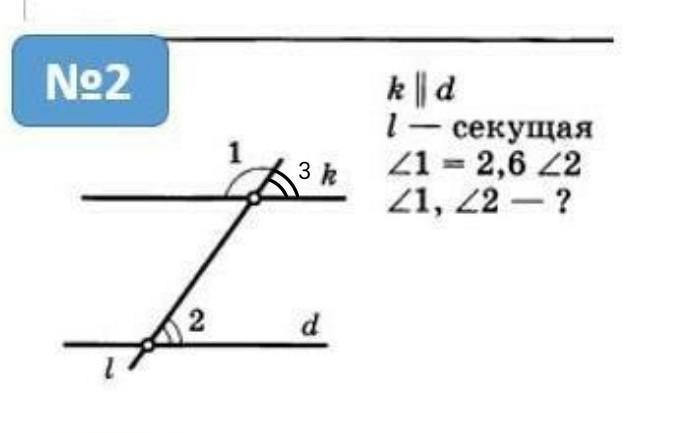
Задание №2.
Дано :
k || d, l — секущая.
∡1 = 2,6×∡2.
Найти :
∡1 = ?
∡2 = ?
Решение :
- При пересечении двух параллельных прямых секущей соответственные углы равны.
Следовательно, ∡2 = ∡3.
В свою очередь ∡1 + ∡3 = 180°, так как они смежные. Но так как ∡2 = ∡3, то ∡1 + ∡2 = 180°.
Тогда —
2,6×∡2 + ∡2 = 180°
3,6×∡2 = 180° | : 3,6
∡2 = 50°
∡1 = 2,6×∡2 = 2,6×50° = 130°.
Ответ :
∡1 = 130°, ∡2 = 50°.
Задание №3.
Дано :
KP || NM.
∡NKP = 120°, ∡NKM = 90°.
Найти :
∡N = ?
∡M = ?
Решение :
- При пересечении двух параллельных прямых секущей сумма внутренних односторонних углов равна 180°.
Рассмотрим параллельные прямые КР и NM при секущей KN. По выше сказанному ∡N + ∡NKP = 180°⇒∡N = 180° - ∡NKP = 180° - 120° = 60°.
Рассмотрим эти же прямые при секущей КМ.
∡NKM + ∡MKP = ∡NKP⇒∡MKP = ∡NKP - ∡NKM = 120° - 90° = 30°.
- При пересечении двух параллельных прямых секущей внутренние накрест лежащие углы равны.
Следовательно, ∡MKP = ∡M = 30°.
Ответ :
∡N = 60°, ∡M = 30°.