Предмет: Алгебра,
автор: beibarys99
Решите эту задачу плиз в 1 первой задаче надо найти а-в
Приложения:
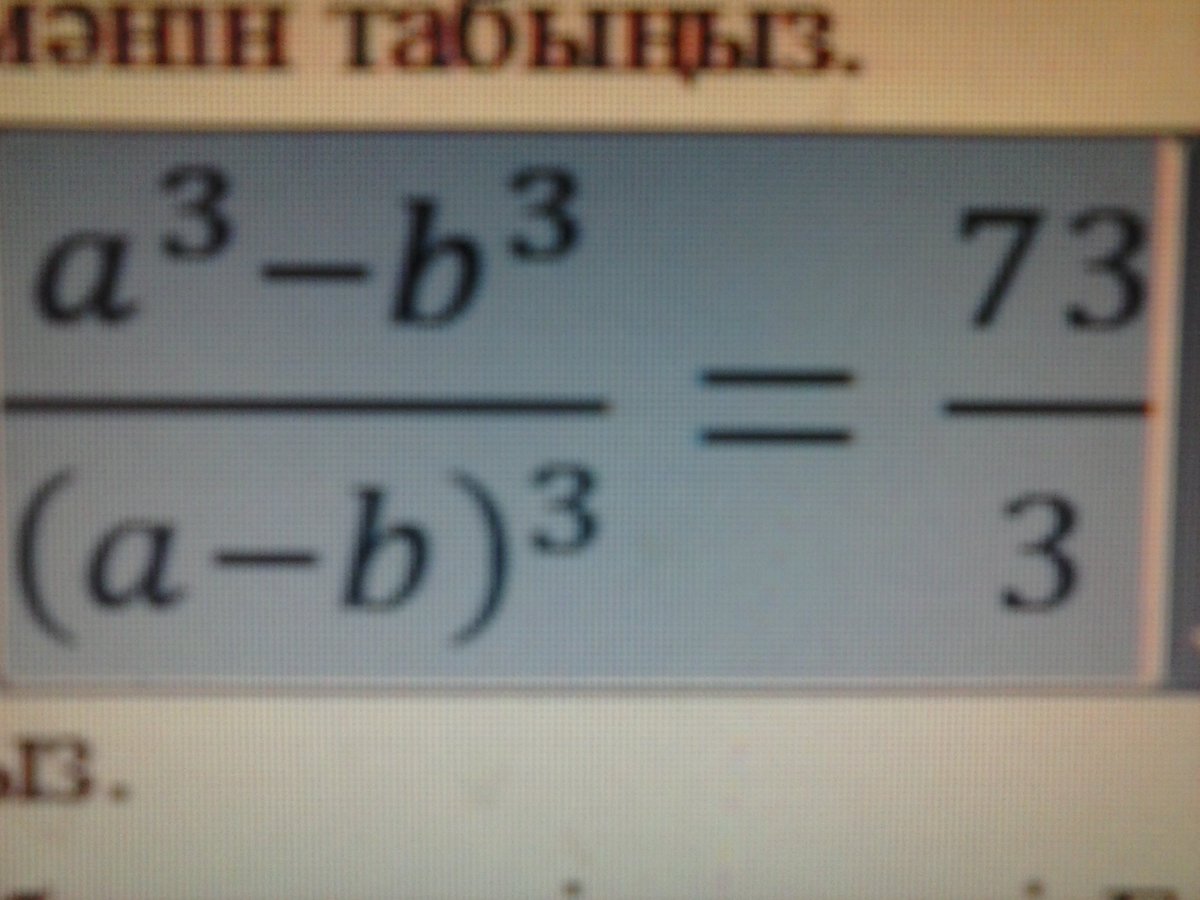
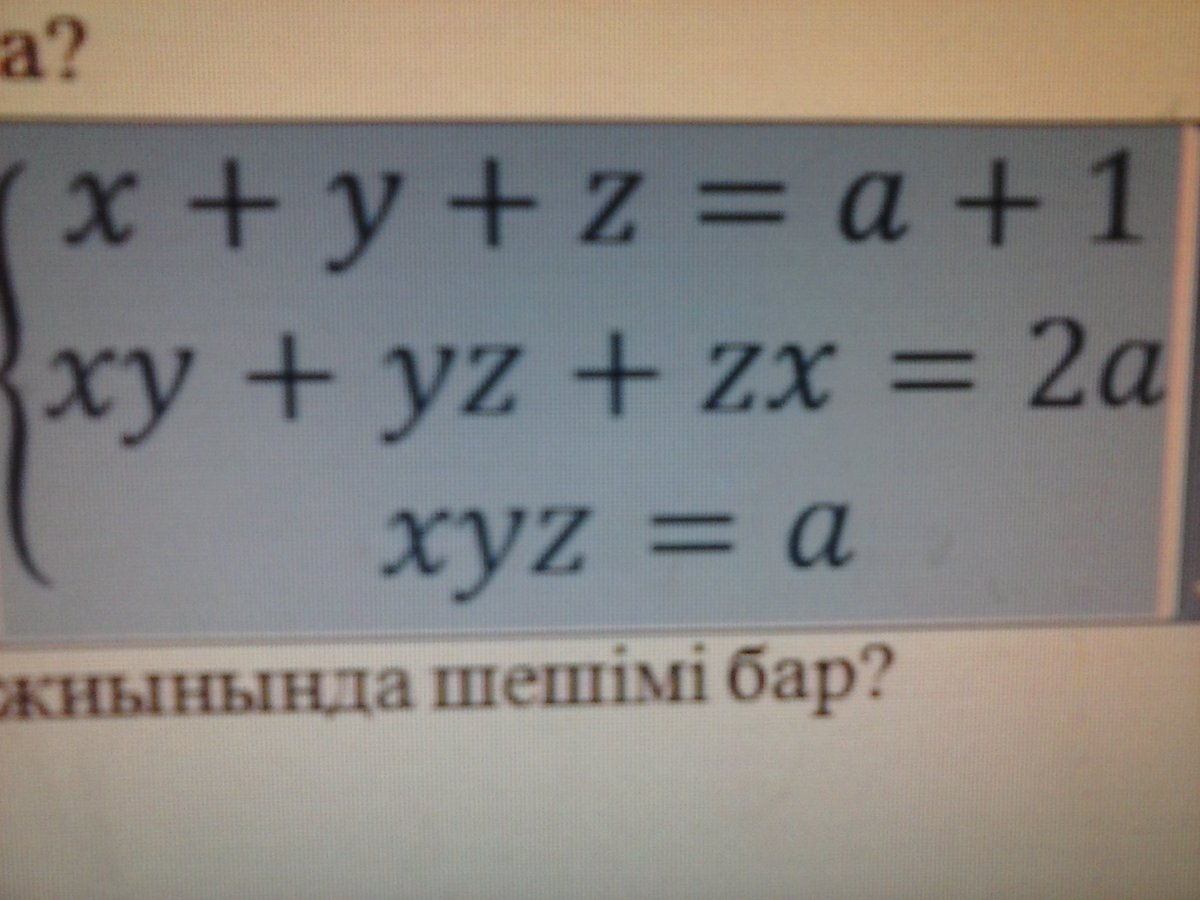
Ответы
Автор ответа:
0
1) (a^3 - b^3)/(a-b)^3 = 73/3
(a-b)(a^2+ab+b^2)/(a-b)^3 = 73/3
(a^2+ab+b^2)/(a-b)^2 = 73/3
(a^2+ab+b^2)/(a^2-2ab+b^2) = 73/3
(a^2-2ab+3ab+b^2)/(a^2-2ab+b^2) = 73/3
1 + 3ab/(a-b)^2 = 1 + 70/3
3ab/(a-b)^2 = 70/3
9ab = 70(a-b)^2
a-b = 3V(ab)/V(70)
Как выразить a-b только в числах, я не знаю.
2) Это проще. Эта система есть теорема Виета для кубического уравнения.
(t-x)(t-y)(t-z) = 0
(t-x)(t^2 - t(y+z) + yz) = 0
t^3 - t^2(x+y+z) + t(xy+xz+yz) - xyz = 0
t^3 - (a+1)t^2 + 2at - a = 0
t^3 - t^2 - a(t^2 - 2t + 1) = 0
t^2*(t-1) - a(t-1)^2 = 0
(t-1)(t^2 - at + a) = 0
t1 = 1
D = a^2 - 4a >= 0
При a < 0 U a > 4 будет 3 корня
t2 = (-a - V(a^2-4a))/2
t3 = (-a + V(a^2-4a))/2
При а = 0 и а = 4 будет 2 корня
t2 = t3 = -a/2
При 0 < a < 4 будет 1 корень t = 1
6 решений:
1) x = 1, y = (-a - V(a^2-4a))/2, z = (-a + V(a^2-4a))/2
2) x = 1, y = (-a + V(a^2-4a))/2, z = (-a - V(a^2-4a))/2
3) x = (-a - V(a^2-4a))/2, y = 1, z = (-a + V(a^2-4a))/2
4) x = (-a + V(a^2-4a))/2, y = 1, z = (-a - V(a^2-4a))/2
5) x = (-a - V(a^2-4a))/2, y = (-a + V(a^2-4a))/2, z = 1
6) x = (-a + V(a^2-4a))/2, y = (-a - V(a^2-4a))/2, z = 1
(a-b)(a^2+ab+b^2)/(a-b)^3 = 73/3
(a^2+ab+b^2)/(a-b)^2 = 73/3
(a^2+ab+b^2)/(a^2-2ab+b^2) = 73/3
(a^2-2ab+3ab+b^2)/(a^2-2ab+b^2) = 73/3
1 + 3ab/(a-b)^2 = 1 + 70/3
3ab/(a-b)^2 = 70/3
9ab = 70(a-b)^2
a-b = 3V(ab)/V(70)
Как выразить a-b только в числах, я не знаю.
2) Это проще. Эта система есть теорема Виета для кубического уравнения.
(t-x)(t-y)(t-z) = 0
(t-x)(t^2 - t(y+z) + yz) = 0
t^3 - t^2(x+y+z) + t(xy+xz+yz) - xyz = 0
t^3 - (a+1)t^2 + 2at - a = 0
t^3 - t^2 - a(t^2 - 2t + 1) = 0
t^2*(t-1) - a(t-1)^2 = 0
(t-1)(t^2 - at + a) = 0
t1 = 1
D = a^2 - 4a >= 0
При a < 0 U a > 4 будет 3 корня
t2 = (-a - V(a^2-4a))/2
t3 = (-a + V(a^2-4a))/2
При а = 0 и а = 4 будет 2 корня
t2 = t3 = -a/2
При 0 < a < 4 будет 1 корень t = 1
6 решений:
1) x = 1, y = (-a - V(a^2-4a))/2, z = (-a + V(a^2-4a))/2
2) x = 1, y = (-a + V(a^2-4a))/2, z = (-a - V(a^2-4a))/2
3) x = (-a - V(a^2-4a))/2, y = 1, z = (-a + V(a^2-4a))/2
4) x = (-a + V(a^2-4a))/2, y = 1, z = (-a - V(a^2-4a))/2
5) x = (-a - V(a^2-4a))/2, y = (-a + V(a^2-4a))/2, z = 1
6) x = (-a + V(a^2-4a))/2, y = (-a - V(a^2-4a))/2, z = 1
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: nurmaganbetovesej
Предмет: Геометрия,
автор: Brimir
Предмет: Алгебра,
автор: AlinaAcorn