Question

Стороны ромба длиной 40 см касаются сферы.

Острый угол ромба равен 60°.

Определи расстояние плоскости ромба от центра сферы, если радиус сферы равен 20 см.

 


​

Answer 1

Ответ:

10 см.

Объяснение:

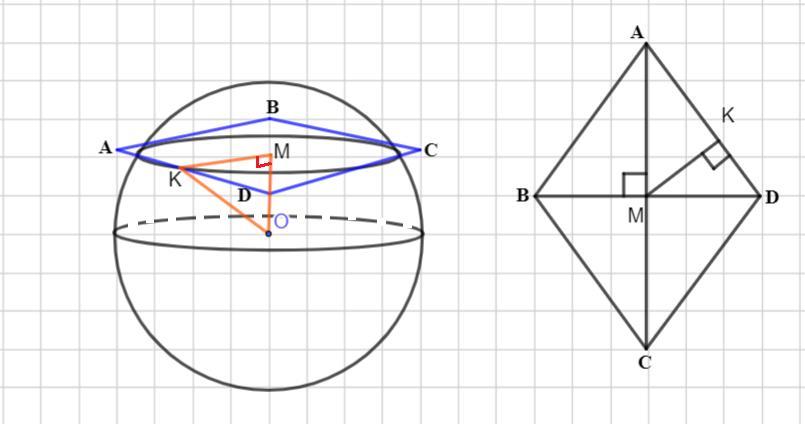
Рассмотрим треугольник КМО - прямоугольный.

Отрезок ОК - радиус сферы. Точка К- точка касания ромба сферы.

ОК= 20 см.

Отрезок МК - радиус вписанной окружности в ромб или высота прямоугольного треугольника AMD.

Радиус окружности вписанной в ромб определяется через площадь

$S=\dfrac{1}{2} P\cdot r;\\\\r=\dfrac{2S}{p}$

По условию сторона ромба равна 40 см, то периметр будет

$P=4\cdot40 =160$ cм.

Площадь ромба найдем по формуле:

$S=a^{2} \sin\alpha ;\\S=40^{2} \cdot \sin60^{0} =1600\cdot \dfrac{\sqrt{3} }{2} =\dfrac{1600\sqrt{3} }{2} =800\sqrt{3}$

800√3 cм²- площадь ромба.

Тогда найдем радиус вписанной в ромб окружности

$r=\dfrac{2\cdot800\sqrt{3} }{160} =\dfrac{1\cdot800\sqrt{3} }{80} =10\sqrt{3}$  см.

Значит, длина отрезка  КМ=10√3 см.

Применим к прямоугольному треугольнику  КМО теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$KO^{2} =KM^{2} +OM^{2} ;\\OM^{2}=KO^{2} -KM^{2};\\OM=\sqrt{KO^{2} -KM^{2}} ;\\OM=\sqrt{20^{2}-(10\sqrt{3} )^{2} } =\sqrt{400-300} =\sqrt{100} =10$

OM= 10 cм