Предмет: Математика,
автор: Егор228элита
помогите срочно решить до завтра
Приложения:
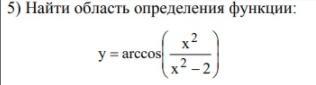
Ответы
Автор ответа:
0
Ответ:
значения косинуса имеют пределы:
значит
решим системой:
рисунок1
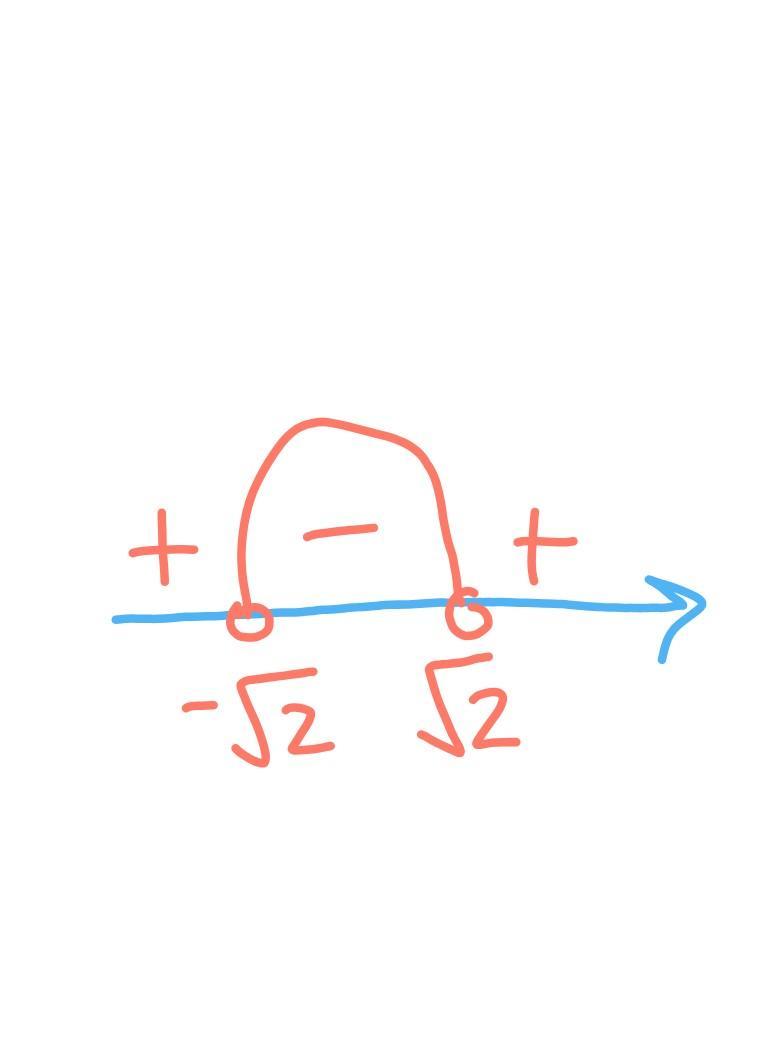
рисунок2
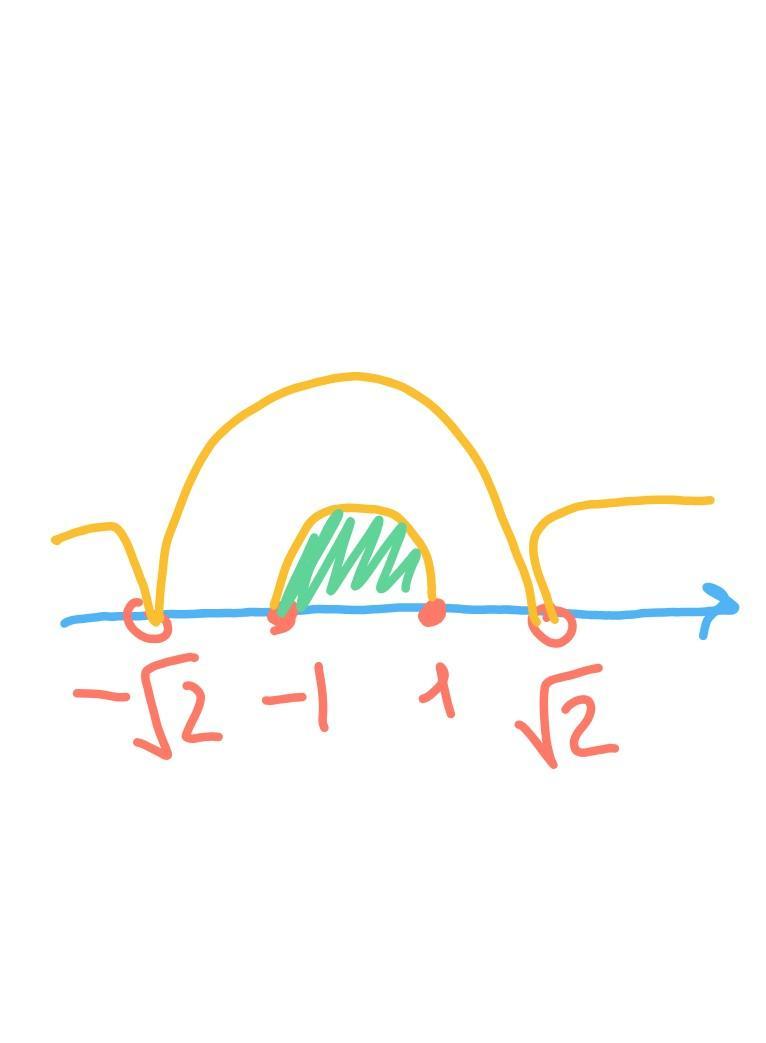
Пересекаем оба промежутка:
рисунок 3
зеленым - область пересечения
Ответ:
Приложения:
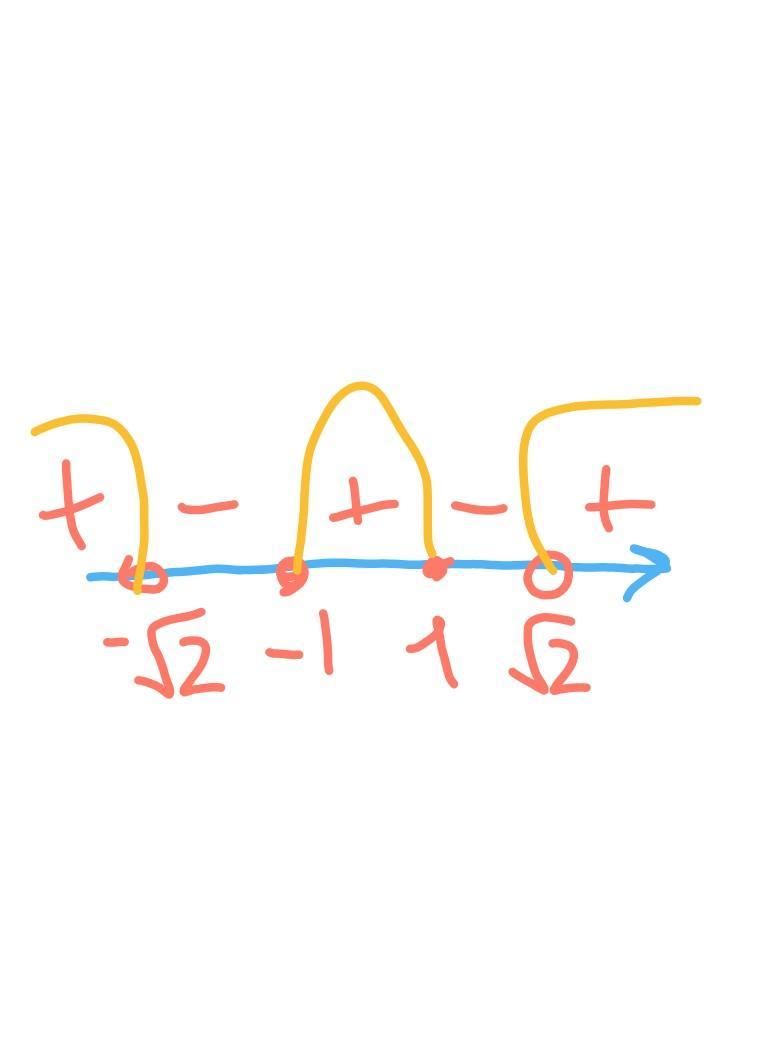
Похожие вопросы
Предмет: Английский язык,
автор: Evreevaa
Предмет: География,
автор: liza5568
Предмет: Українська література,
автор: natashka2265
Предмет: Қазақ тiлi,
автор: sarsenzhakarova
Предмет: Обществознание,
автор: felekskilSOVERGON