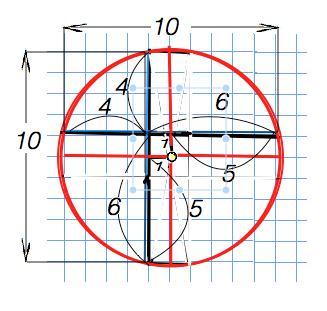
В окружности проведены две взаимно перпендикулярные хорды.Каждая из них делится другой хордой на отрезки, равные 4 и 6. Найдите расстояние от центра окружности до каждой хорды.
Ответы
Перпендикуляр, проведенный из центра окружности к хорде, делит эту хорду и стягиваемые ею дуги пополам.
Перпендикулярами хорды делятся на две равные части по (4+2):2=3.
Отрезки с частями хорд от точки пересечения хорд до точки пересечения с перпендикулярами из центра окружности образуют квадрат со стороной 1 - расстоянием до каждой хорды.
Ответ: 1 (ед. длины)
Объяснение:
Чтобы найти расстояние от центра окружности до каждой хорды, проведем через середину каждой перпендикулярно по прямой. Прямая, проведенная перпендикулярно хорде через середину, проходит через центр окружности и содержит диаметр окружности ( свойство). При этом пересекающиеся хорды и пересекающиеся диаметры ( которые будут параллельны хордам и взаимно перпендикулярны) образуют квадратик со сторонами, равными разности между бóльшим отрезком, на которые хорды делятся при пересечении, и их половинами. Длина каждой хорды 6+4, их половин 10:2.
6 - (6+4):2 =1. (См. рисунок приложения)