Предмет: Алгебра,
автор: spacegrace67
Найдите производные функций
ХЕЛП ПЛИИИИЗ
Приложения:
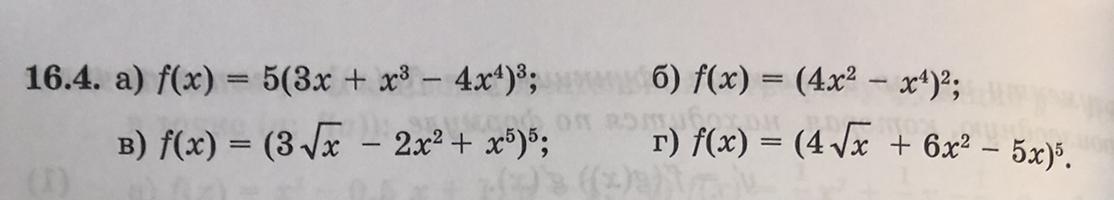
Ответы
Автор ответа:
1
Ответ:
а)
б)
в)
г)
spacegrace67:
спасибо большое
а ты можешь пожалуйста ещё решить 16.3 , у меня в вопросах есть этот номер
привет! Это снова я, у меня в вопросах есть 17.9 и 17.10 реши пожалуйста , ты всегда меня очень выручаешь
Похожие вопросы
Предмет: Математика,
автор: rampage968
Предмет: Литература,
автор: cenblock830
Предмет: Математика,
автор: AlionaFab12
Предмет: Химия,
автор: baddika79
Предмет: Физика,
автор: Аноним