Предмет: Геометрия,
автор: avuk45milon
Точка D находится на расстоянии 17 см от каждой вершины прямоугольного треугольника АВС (∠ACB = 90°). Найдите расстояние от точки D до плоскости АВС, если АС = 10√2 см, ВС = 2√14 см.
Ответы
Автор ответа:
13
Ответ:
Расстояние от точки D до плоскости АВС 15 см.
DO = 15 см.
Объяснение:
Дано: ∠ACB = 90°, DO ⊥ ABC, AD = BD = CD = 17 см, см,
см
Найти: DO - ?
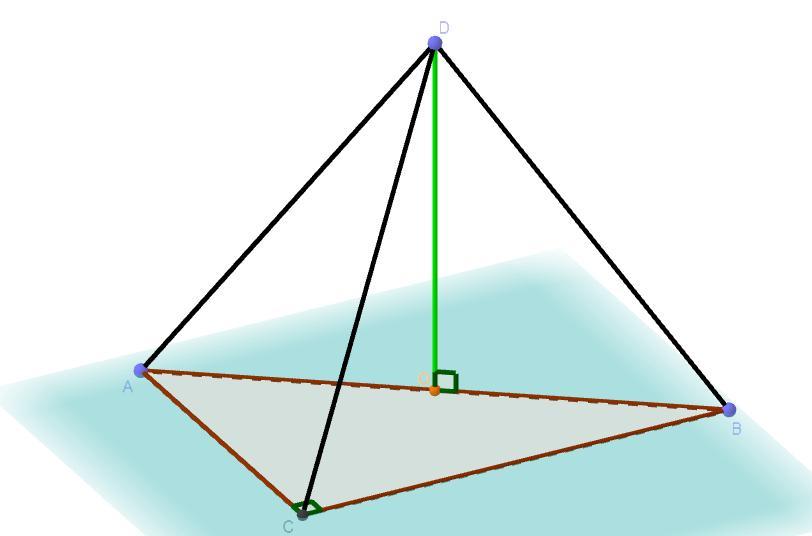
Решение: Так как точка D равноудалена от каждой вершины треугольника(по условию AD = BD = CD), то согласно теореме она проектируется в центр описанной окружности треугольника. Так как центр описанной окружности лежит на гипотенузе и делит гипотенузу пополам, то точка D проектируется в точку O которая является серединой гипотенузы AB. Рассмотрим прямоугольный треугольник ΔABC(по условию ∠ABC = 90°). По теореме Пифагора: см.
Так как точка O является серединой гипотенузы AB, то AO = OB =
AB : 2 = 16 : 2 = 8 см. Треугольник ΔAOD - прямоугольный так как DO ⊥ ABC по условию. По теореме Пифагора: см.
Приложения:
Похожие вопросы
Предмет: География,
автор: gbcmrf1998
Предмет: Алгебра,
автор: MichaelNik
Предмет: Химия,
автор: qswdef911
Предмет: Русский язык,
автор: mishkud
Предмет: Українська мова,
автор: litlprincess