выбери верные утверждения для функции у-2х^2+20x+5
Верных ответов: 6
Нули функции x1,2 =10+-корень110/2
Промежуток убывания x ∈ [5; +∞).
Наибольшее значение функции – y = 55.
Промежуток возрастания x ∈ (–∞; 55].
Ветви параболы направлены вниз.
Вершина параболы – точка (5; 55).
Множество значений функции: (–∞; +∞).
График функции проходит через точку (3; 37).
Область определения функции: (5; +∞).
Прямая x = 5 является осью симметрии графика функции.
Ответы
Ответ:
Нули функции
.
Промежуток убывания x ∈ [5; +∞).
Наибольшее значение функции – y = 55.
Вершина параболы – точка (5; 55).
Прямая x = 5 является осью симметрии графика функции.
Ветви параболы направлены вниз.
Объяснение:
Проведем исследование функции
1. Область определения функции
D(y) = R (так как в функцию можно подставить любые значения x)
2. Исследовать функцию на парность
Ни четная, ни нечетная
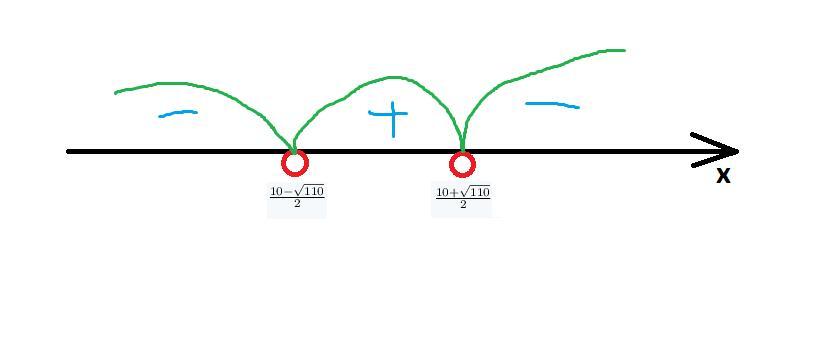
3. Найти нули функции
4. Промежутки знакопостоянства функции
при
при
5. Исследовать функцию на непрерывность
Так как D(y) ∈ R, то у функции нет разрывов следовательно функция y непрерывна на D(y) ∈ R.
6. Найти асимптоты
Так как функция y непрерывна, то функция не имеет асимптот
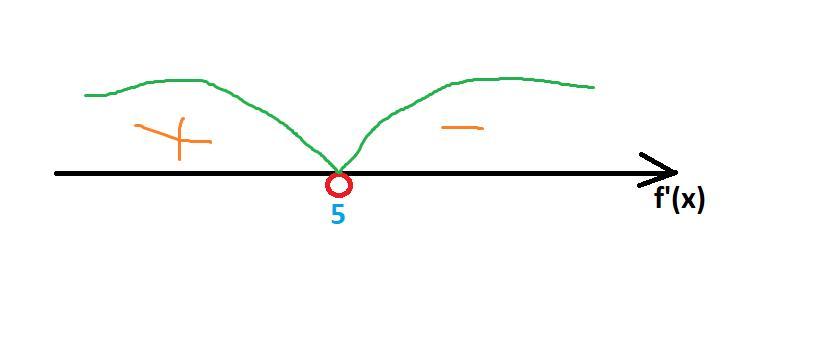
7. Найти промежутки возрастания и убывания функции
При функция убывает
При функция возрастает
8.
при
и так как:
При функция убывает
При функция возрастает
То точка x = 5 является экстремумом и локальным максимумом функции
max: y(5) = -2 * 5² + 20 * 5 + 5 = -50 + 100 + 5 = 55
9. Найти промежутки выпуклости и точки перегиба
Так как , то функция выпукла вверх при x ∈ R.
Функция не имеет точек перегиба.
10. Найти область значений функции:
11. Особые свойства функции
Вершиной параболы является точка в которой производная квадратичной функции равна нулю.
Вершина параболы
Проходит парабола через точку (3;37)
y(3) = -2 * 3² + 20 * 3 + 5 = -18 + 60 + 5 = 47
следовательно график функции y не проходит через точку (3;37).
Ось симметрии параболы параллельна оси ординат и проходит через вершину параболы, следовательно уравнение оси симметрии параболы x = 5.
Так как a < 0 (-2 < 0), то ветви параболы направлены вниз.
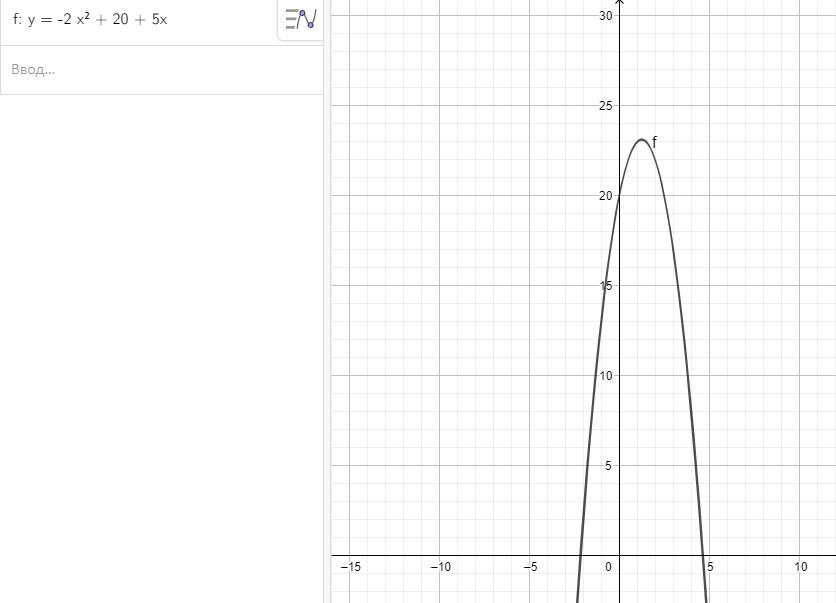
Нули функции x1,2 =
Наибольшее значение функции – y = 55.
Промежуток убывания x ∈ [5; +∞).
Вершина параболы – точка (5; 55).
Ветви параболы направлены вниз.