Question

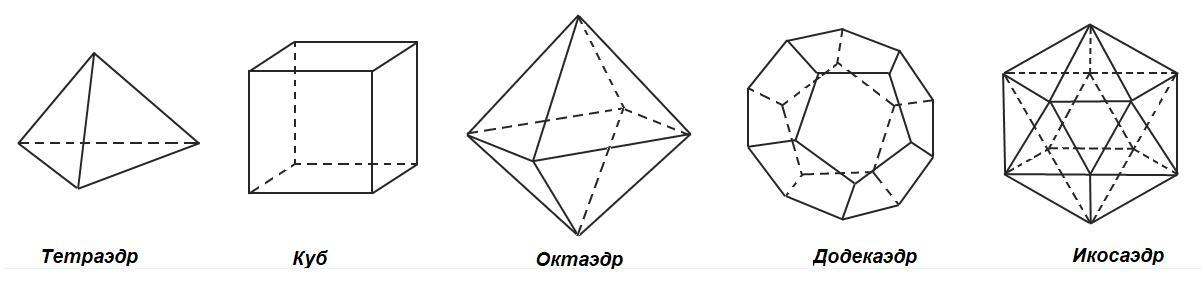
1. Многогранник, составленный из четырех правильных многоугольников:

А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр


2. Многогранник, каждая вершина которого является вершиной трех квадратов:

А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр


3. Многогранник, составленный из пятиугольников:

А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр


4. Многогранник, составленный из восьми треугольников:

А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр


5. Многогранник, каждая вершина которого является вершиной пяти треугольников:

А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр


6. Многогранник, сумма плоских углов при каждой вершине которого равна 3000:

А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр


7. Многогранник, сумма плоских углов при каждой вершине которого равна 3240:

А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
​

Answer 1

Ответ:

1. А)

2. В)

3. Е)

4. С)

5. D)

6. D)

7. E)

Объяснение:

1. Многогранник, составленный из четырех правильных многоугольников:

А) Тетраэдр

2. Многогранник, каждая вершина которого является вершиной трех квадратов:

В) Куб  

3. Многогранник, составленный из пятиугольников:

Е) Додекаэдр

4. Многогранник, составленный из восьми треугольников:

С) Октаэдр

5. Многогранник, каждая вершина которого является вершиной пяти треугольников:

D) Икосаэдр

6. Многогранник, сумма плоских углов при каждой вершине которого равна 300°:

D) Икосаэдр

Каждая грань икосаэдра - правильный треугольник, каждый угол которого равен 60°. Так как в вершине сходятся 5 треугольников, то

60° · 5 = 300°

7. Многогранник, сумма плоских углов при каждой вершине которого равна 324°:

Е) Додекаэдр

Каждая ​грань додекаэдра - правильный пятиугольник. Угол правильного пятиугольника:

$\dfrac{180^\circ(5-2)}{5}=\dfrac{180^\circ\cdot 3}{5}=\dfrac{540^\circ}{5}=108^\circ$

Тогда сумма углов при одной вершине:

108° · 3 = 324°