Question

через перпендикулярность а не Пифагора ​
доказать что bc перпендикулярна ac

Answer 1

Ответ:

7.

Объяснение:

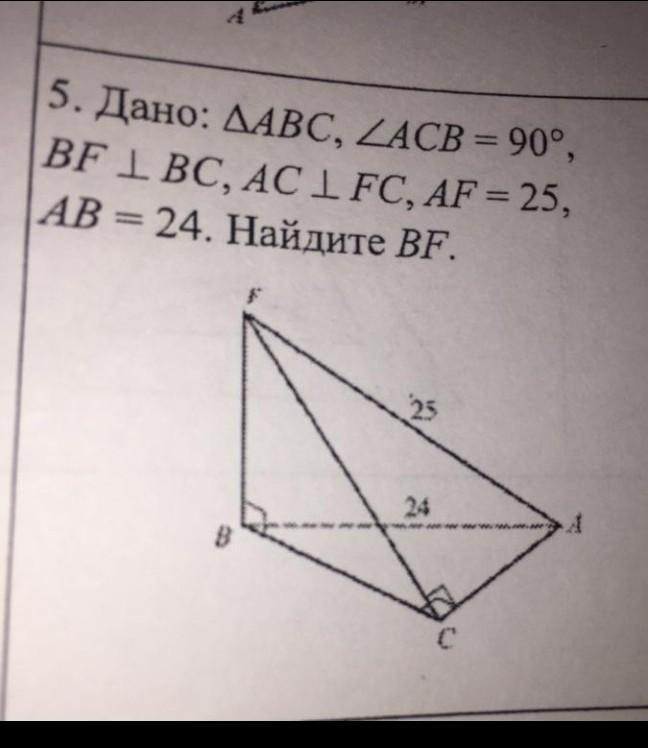
1) По условию АС ⟂ СВ, АС ⟂ СF, CB⋂CF, тогда по признаку перпендикулярности прямой и плоскости АС ⟂ (FBC), а значит и любой прямой, лежащей в этой плоскости, АС ⟂ ВF.

2) ВF ⟂ АС (см. п. 1), ВF ⟂ ВС (по условию), АC⋂ВC, тогда по признаку перпендикулярности прямой и плоскости ВF ⟂ (ABC), а значит и любой прямой, лежащей в этой плоскости. Получили , что ВF ⟂ BA

3) В ∆ FBA по теореме Пифагора

ВF² = FA² - AB² = 25² - 24² = 49

BF = √49 = 7.